Дополнение 2 к главе 3. Обращение блочных матриц

Рассмотрим обращение некоторых блочных матриц.

Пусть

– невырожденная квазидиагональная матрица с квадратными блоками A и D. Из невырожденности следует, что detA0 и detD0. Пусть

– обратная матрица, разбитая на блоки в соответствии с разбиением исходной матрицы. Из равенства

следует уравнения

.

Из первого уравнения находим , из второго Y=0, из четвертого и, наконец, из третьего . Итак,

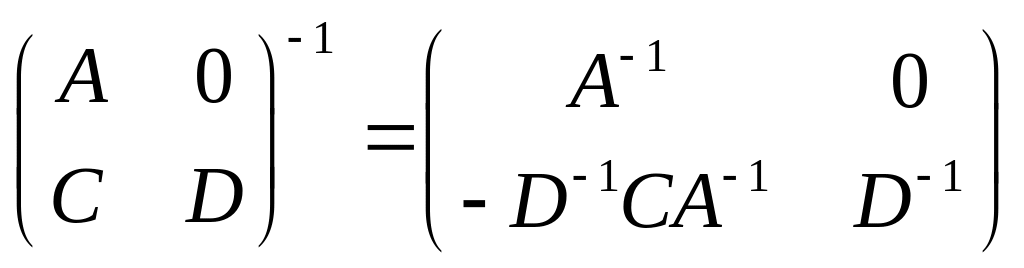. (3.17)

Аналогично,

. (3.18)

Пусть дана невырожденная матрица

,

где A и D – квадратные блоки. Умножим матрицу слева на матрицу

,

получим

.

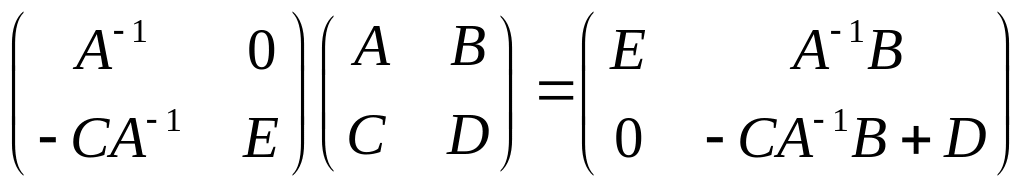Перейдем в этом равенстве к обратным матрицам:

.

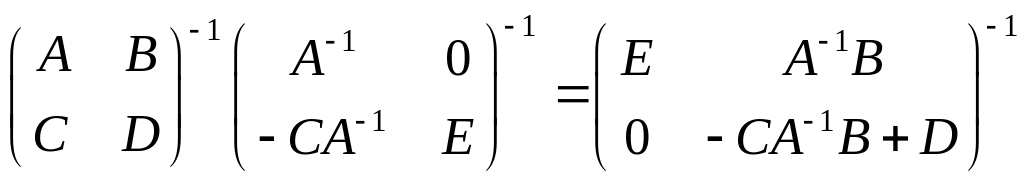Используя формулу (3.17), получим

.

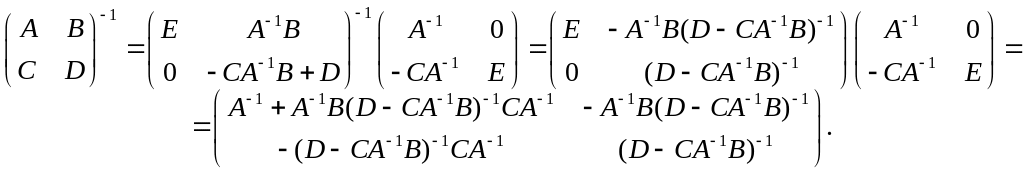Таким образом, результат можно записать в виде

, (3.19)

где

(3.20)

или

(3.21)

Эти формулы называются формулами Фробениуса. Предполагая, что указанные здесь обратные матрицы существуют, можно свести вычисление обратной матрицы порядка k+l к вычислению одной обратной матрицы порядка k и одной матрицы порядка l.

Пример 3.6. Найти обратные матрицы для следующих матриц:

а) 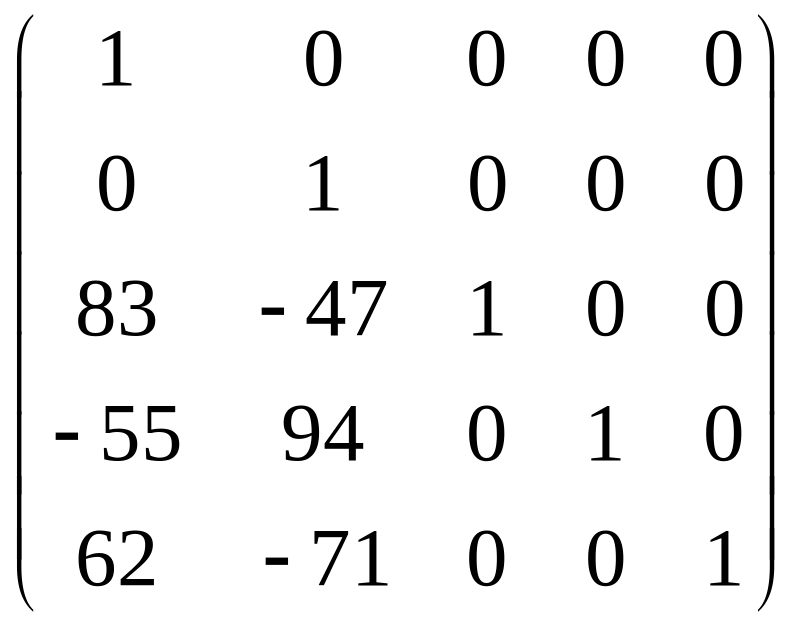, б) .

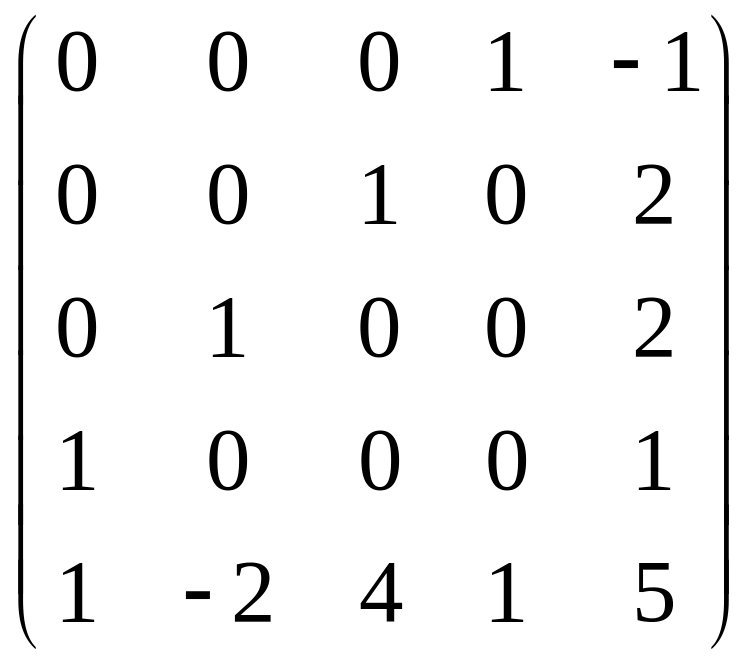Решение. а) Воспользуемся формулой (3.17), где

, , .

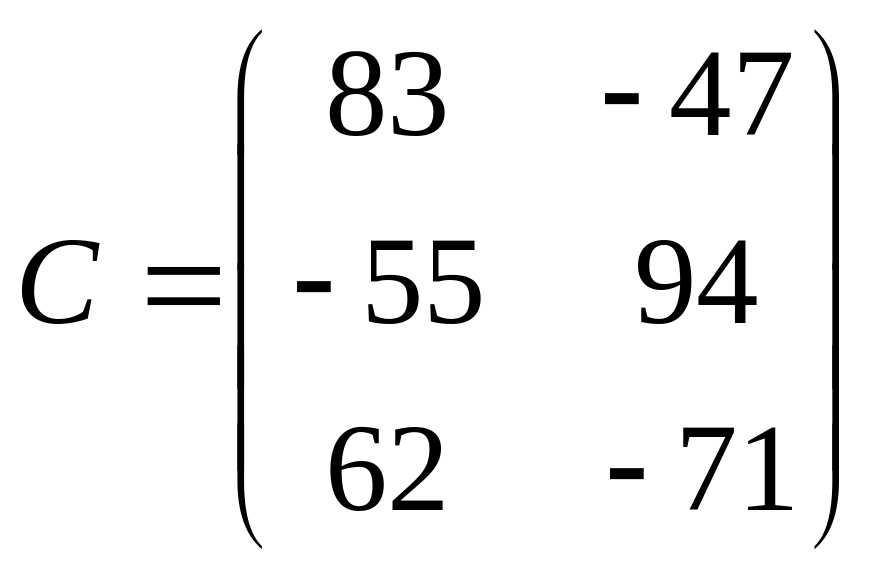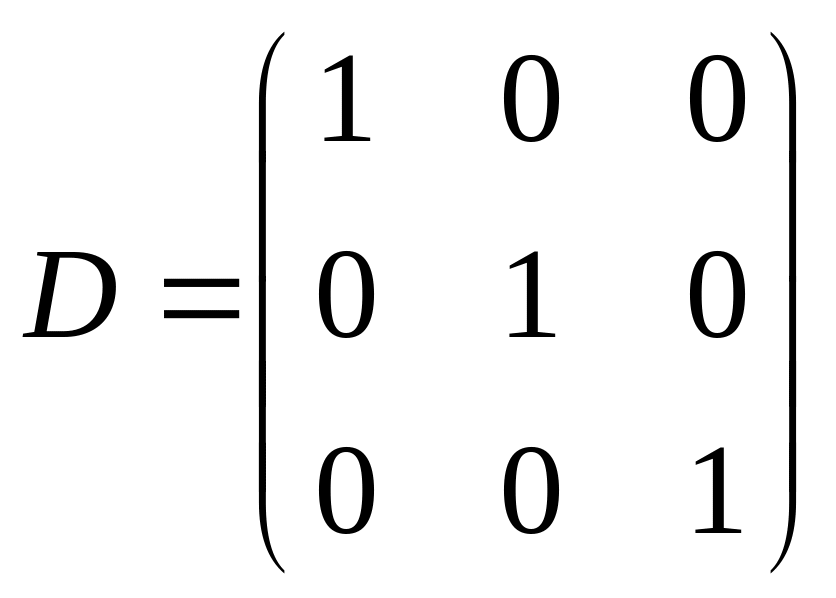Поскольку A и D – единичные матрицы, то . В результате получаем

.

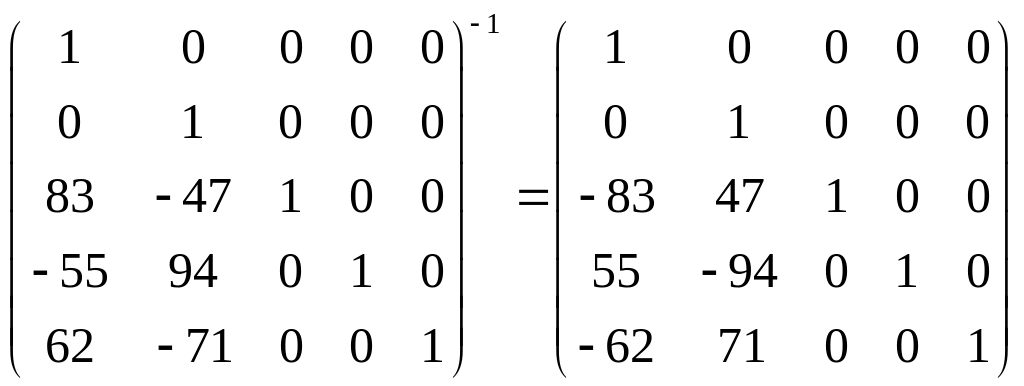
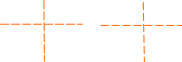б) Воспользуемся формулой Фробениуса (3.20), где

, , , .

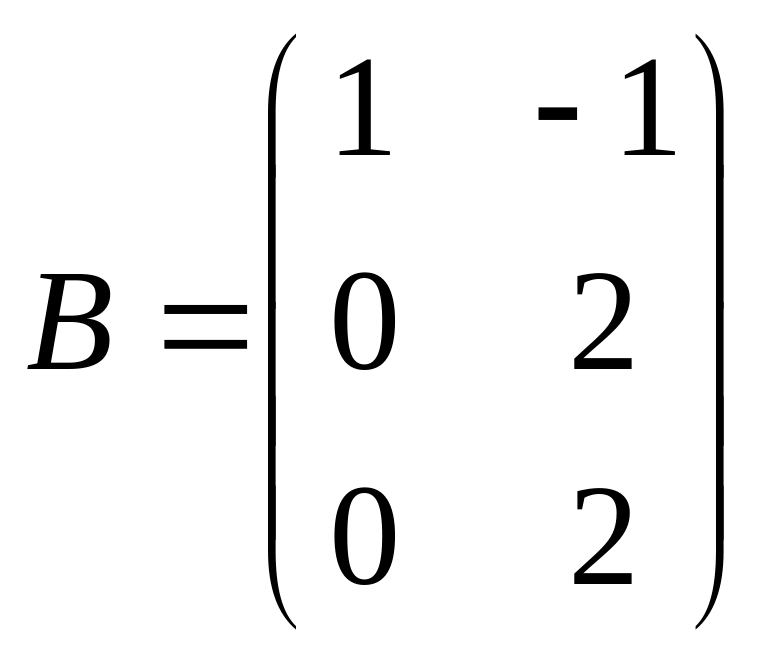Поскольку

, , ,

, ,

, .

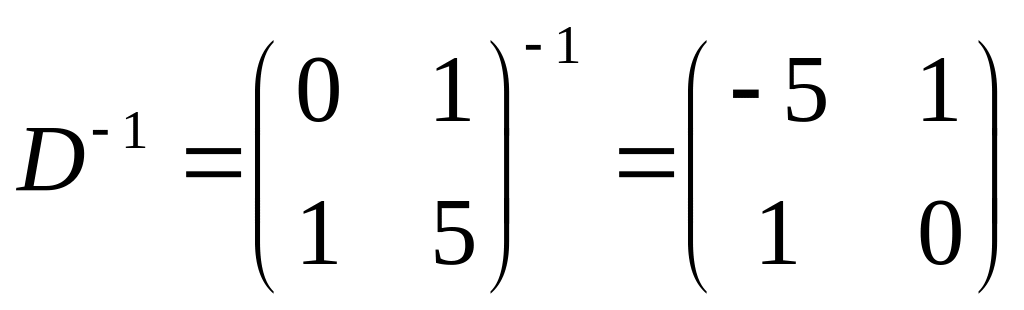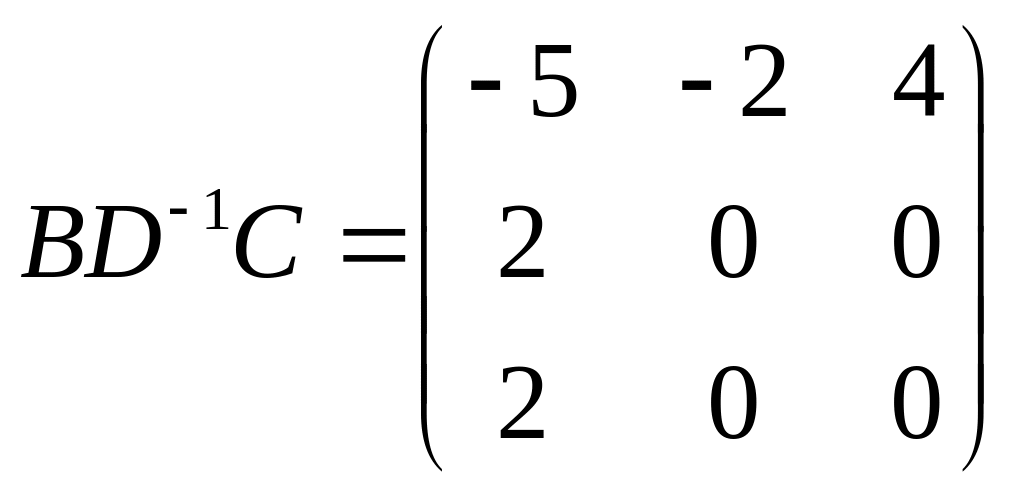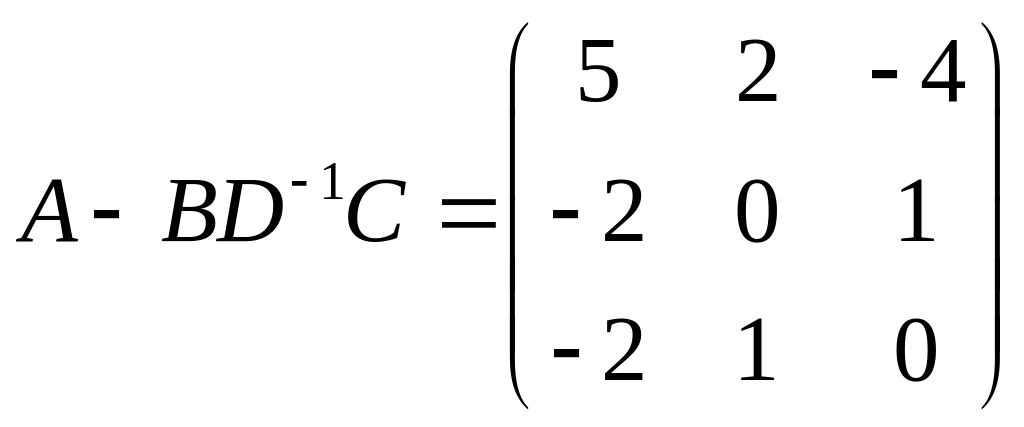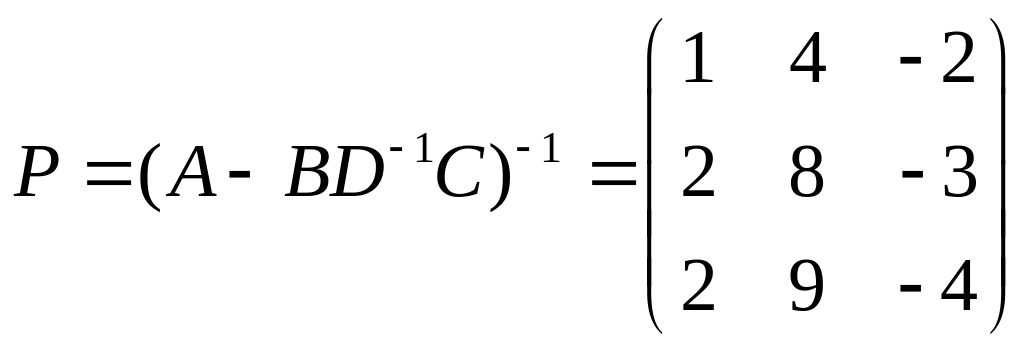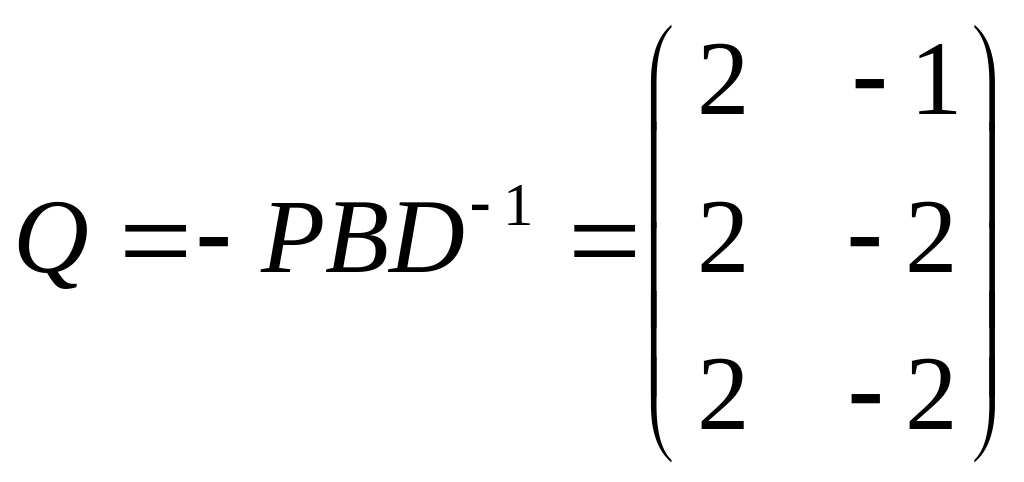Таким образом,

.

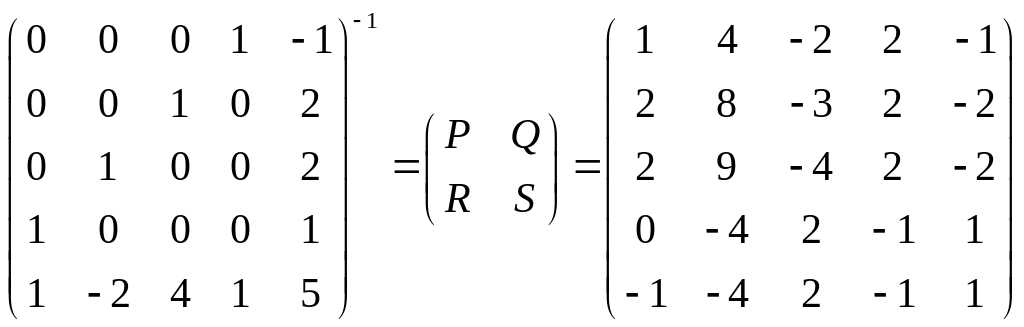
Дополнение 3 к главе 3. Ортогональные матрицы

Квадратную матрицу O называют ортогональной, если её обратная матрица совпадает с транспортированной:

. (3.22)

Например, простейшей ортогональной матрицей является единичная матрица E, так как . Ортогональные матрицы второго порядка имеют вид

.

Из определения ортогональной матрицы вытекает ряд свойств.

1. Ортогональная матрица O удовлетворяет равенству: .

 Действительно умножая равенство (3.22) слева на матрицу O, получим , или ; умножая равенство (3.22) права на матрицу O, получим , или . 

2. Ортогональность матрицы O влечёт ортогональность матрицы .

 Действительно из равенства следует . 

3. Ортогональность матрицы O влечёт ортогональность матрицы .

 Действительно, , ортогональность уже доказана. 

4. Произведение двух ортогональных матриц одного порядка тоже является ортогональной матрицей.

 Действительно, пусть O и Q – ортогональные матрицы. Тогда

. 

5. Определитель ортогональной матрицы равен .

 Действительно, , откуда следует . 

Ортогональные матрицы разбиваются на два класса – собственно ортогональные с определителем 1, и несобственно ортогональные с определителем –1. В дальнейшем мы увидим различие в геометрическом смысле собственно и несобственно ортогональных матриц.