Матричные уравнения a) Решение матричных уравнений
На практике часто встречаются различные матричные уравнения. Простейшими из них являются уравнения вида
,
(3.13)
,
(3.14)
где A и B – данные квадратные матрицы n-го порядка, а X – искомая матрица того же порядка.
Решением
матричного уравнения называется всякая
матрица соответствующего порядка,
которая, будучи подставлена в матричное
уравнение вместо матрицы X,
обращает уравнение в тождество. Матричные
уравнения (3.13) и (3.14) имеют единственные
решения, если матрица A
невырождена:
.
Действительно, умножив эти уравнения
соответственно слева и справа на матрицу
A–1,
получим
,
(3.15)
.
(3.16)
Рассмотренные уравнения легко обобщаются на случай нескольких матриц. Например, рассмотрим уравнение
ABXC = D,
где A, B, C – невырожденные матрицы. Преобразуя это уравнение, получим
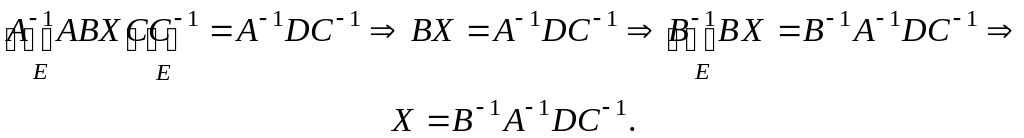
Пример 3.4. Решить матричное уравнение
Решение. Данное уравнение коротко можно записать следующим образом: AX=B. Тогда решение будет иметь вид X=A–1B, т.е.
Поскольку
то
Следовательно,
.
*Для решения уравнений (3.13) и (3.14) можно использовать и метод элементарных преобразований.
Для
уравнения (3.13) этот метод основан на
элементарных
преобразованиях строк
расширенной матрицы
и имеет своей целью преобразование её
к виду
,
в котором вместо матрицы A
стоит единичная
матрица E.
Тогда матрица B1
и будет решением уравнения.
Например, найдём решение уравнения в примере 3.4. Выпишем расширенную матрицу и произведем элементарные преобразования над ней:
.
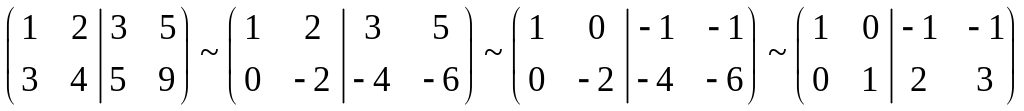Итак,
.
Матричное уравнение (3.14) также можно решить методом элементарных преобразований. Для этого транспонируем обе части равенства
.
После
введения новой неизвестной матрицы
получаем уравнение вида
,
которое решается методом элементарных
преобразований.
Если матрица А – вырожденная или является прямоугольной, то изложенные способы решения матричных уравнений будут непригодными. В этом случае матричное уравнение или имеет бесконечно много решений, или вообще не имеет решений.
B) Матричный способ решения систем линейных уравнений
Любую систему линейных уравнений можно записать в матричном виде AX=B. Если основная матрица системы А – невырожденная, то решение можно записать следующим образом X=A–1B. Записанное равенство составляет сущность матричного решения систем линейных уравнений.
Пример 3.5. Решить систему линейных уравнений при помощи обратной матрицы
Решение. Запишем систему в матричном виде
Найдем обратную матрицу. Поскольку
то
Тогда
Используя обратную матрицу, легко доказать теорему Крамера. Действительно, решение любой квадратной системы линейных уравнений можно записать в виде X=A–1B, если detA0. Существование и единственность решения следует из существования и единственности обратной матрицы. Поэтому выведем формулы Крамера, для этого решение запишем в развернутом виде, используя присоединенную матрицу
Учитывая, что detA=, получим после умножения матриц
откуда следует, что
Выражение в скобках есть разложение определителя по i-му столбцу матрицы, полученной из основной заменой i-го столбца столбцом свободных членов. В результате, получаются формулы Крамера.