15

Глава 3. ОБРАТНАЯ МАТРИЦА

3. Обратная матрица

   1. Обратная матрица и её свойства a) Определение обратной матрицы

Для данной матрицы A правой обратной называется такая матрица B, что . Соответственно, матрица C называется левой матрицей для A, если . Матрица называется обратной для A, если она одновременно левая и правая обратная. Обозначаются обратные матрицы символом A^–1.

Матрица А^–1 называется обратной матрицей по отношению к матрице А, если выполняется равенство

AA^–1 = A^–1A = E. (3.1)

Из данного определения следует, что взаимообратные матрицы перестановочны. Это означает, что только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную.

Теорема 3.1. Если обратная матрица существует, то такая матрица только одна.

 Действительно, пусть существует еще одна матрица В, удовлетворяющая условию АВ=ВА=Е, тогда можно написать:

BAA^–1=(BA)A^–1=EA^–1=A^–1,

BAA^–1=B(AA^–1)=BE=B,

откуда получаем В=А^–1, т.е. обратные матрицы совпадают. 

Теорема 3.2 (теорема замещения). Сумма произведений произвольных чисел b₁, b₂, …, b_n соответственно на алгебраические дополнения элементов некоторой строки (столбца) какого-либо определителя n-го порядка равна определителю, который получается из исходного заменой этой строки (столбца) числами b₁, b₂, …, b_n.

 Возьмём определитель  n-го порядка и выделим в нём какую-либо строку или столбец. Пусть это будет, например, k-я строка:

.

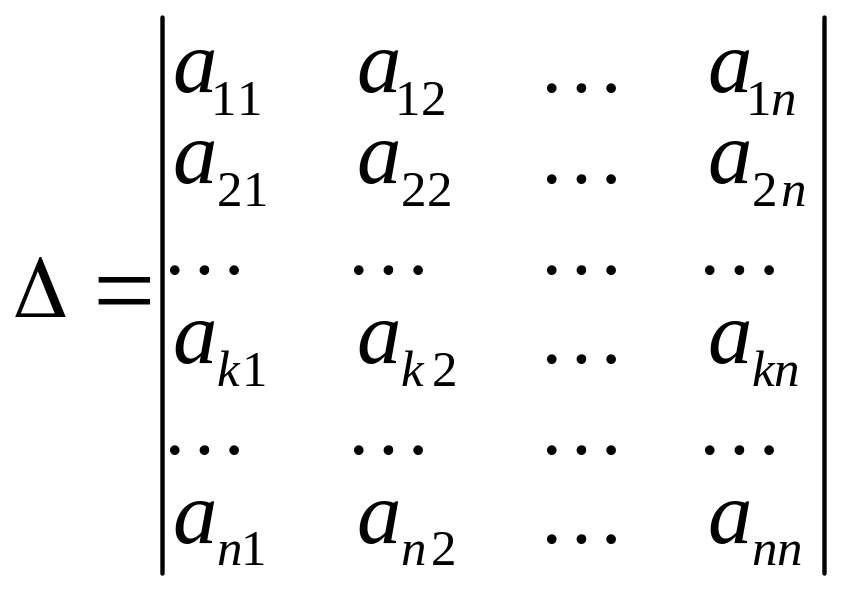Обозначим, как обычно, алгебраические дополнения его элементов через A_ik. Теорема содержит утверждение, что

, (3.2)

где

.

Для доказательства равенства (3.2) заметим, что алгебраические дополнения соответствующих элементов k-й строки определителей  и ₁ одинаковы, ибо при нахождении алгебраических дополнений k-я строка вычеркивается, а в остальном определители совпадают. Следовательно, применяя к определителю ₁ теорему разложения по элементам k-й строки, получаем равенство

,

совпадающее с (3.2). 

Теорема 3.3 (теорема аннулирования). Сумма произведений элементов какой-либо строки (столбца) определителя матрицы A на алгебраические дополнения, соответствующие элементам другой строки (столбца) этого же определителя, равна нулю:

; (3.3)

. (3.4)

 Возьмём в теореме замещения в качестве чисел b₁, b₂, …, b_n элементы l-ой строки определителя . Тогда равенство (3.2) примет вид:

,

где

.

Ясно, что D₁=0, т.к. в этом определителе k-я и l-я строки совпадают. Следовательно,

. 

Теорема 3.4. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля: detA0.

 Необходимость. Действительно, из определения обратной матрицы и свойств определителей получаем: det(A^–1A)=detA^–1detA=detE=1, откуда следует необходимое условие существования обратной матрицы: detA0 или detA^–10.

Достаточность. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для этого нужно указать алгоритм построения такой матрицы. Пусть detA0. Построим новую матрицу следующим образом:

, (3.5)

где Aij – алгебраическое дополнение элемента a_ij матрицы A. Очевидно, что для построения матрицы необходимо сначала заменить элементы матрицы A соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать. Построенная таким образом матрица называется присоединенной к матрице A.

Рассмотрим произведение матриц A и :

.

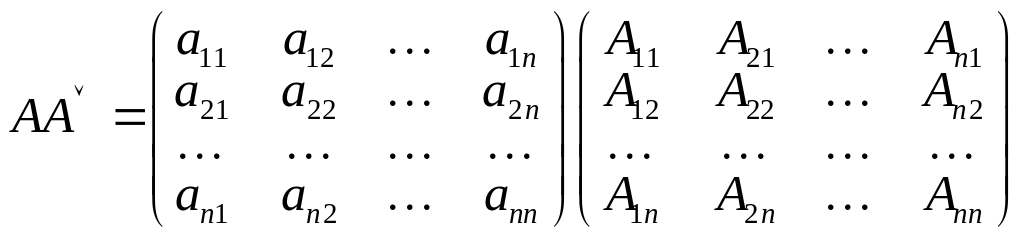Вычисляя общий элемент матрицы по правилу умножения матриц, получим, что он равен

. (3.6)

Но сумма произведений элементов некоторой строки определителя на их алгебраические дополнения равна определителю, а сумма произведений элементов некоторой строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.

,

где

(3.7)

называемый символом Кронекера. Поэтому в результате перемножения матриц A и A^ будет получена скалярная матрица

.

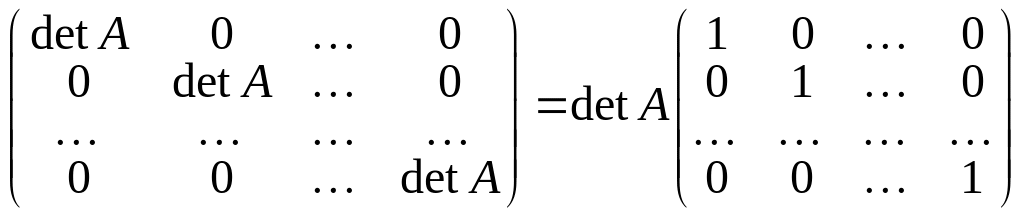Следовательно,

. (3.7)

Аналогичным путём устанавливается равенство

. (3.8)

Таким образом, установлено основное свойство присоединённой матрицы A^, выражаемое равенствами (3.7) и (3.8). Из этих равенств следует, что матрица

(3.9)

будет обратной для матрицы A. 

Матрица, определитель которой отличен от нуля, называется невырожденной, или неособенной; в противном случае она называется вырожденной, или особенной. Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.

Замечание. Отметим, что обобщением обратной матрицы является псевдообратная матрица. Если А – квадратная и неособенная матрица, то для нее существует обратная матрица А^–1. Если же А — не квадратная, а прямоугольная или квадратная, но особенная, матрица, то матрица А не имеет обратной и символ А^–1 не имеет смысла. Однако для произвольной прямоугольной матрицы А существует «псевдообратная» матрица, которая обладает некоторыми свойствами обратной матрицы и имеет важные применения при решении систем линейных уравнений. В случае, когда А – квадратная неособенная матрица, то псевдообратная матрица совпадает с обратной.