6. Расчет элементов таврового сечения.

Расчет элементов таврового сечения. Расчеты прочности многопустотных и ребристых плит перекрытий сводятся к расчету таврового сечения (рис. 13). Основное преимущество таврового сечения перед прямоугольным – это отсутствие «лишнего» бетона в растянутой зоне, поэтому в сравнении с прямоугольным тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности (бетон растянутой зоны не влияет на несущую способность) расход бетона значительно меньше.

Рис. 13.

Два расчетных случая в элементах таврового профиля

Расчетный случай зависит от положения границы сжатой зоны бетона.

1 случай. Граница сжатой зоны проходит в полке . В этом случае тавровое сечение рассчитывают как прямоугольное с размерами (рис. 14), поскольку бетон в растянутой зоне на несущую способность не влияет.

Рис. 14.

2 случай. Граница сжатой зоны находится в ребре (рис. 15). Расчет проводят по формулам таврового профиля.

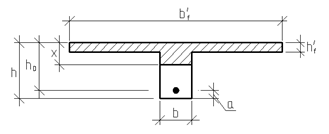
Рис. 15.

Проекция сил, согласно законам статики, приводит к следующим уравнениями с двумя неизвестными:

Определение расчетного случая

Предполагают, что нижняя граница сжатой зоны проходит по нижней грани полки (рис. 16), определяют величину несущей способности таврового сечения на изгиб и сравнивают с величиной изгибающего момента от действия внешних нагрузок.

- граница сжатой зоны находится в полке;

- граница сжатой зоны находится в ребре.

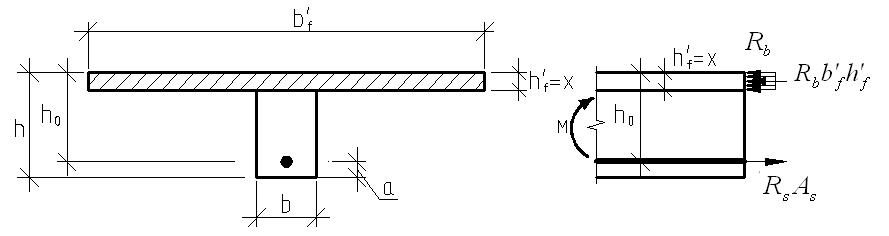
Рис. 16.

7. Свойства бетона при краткосрочном нагружении.

Деформации бетона. При однократном осевом сжатии полная относительная деформация составляет:

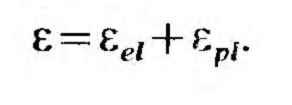
После разгрузки относительные деформации составят:

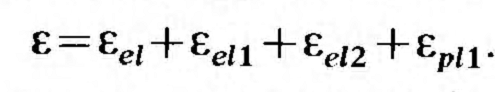
где - упругая деформация, характеризующая частичное восстановление первоначальных размеров образца после разгрузки; - пластическая (неупругая деформация); - упругая составляющая деформации, характеризующая обратимое сплющивание пустот бетона; - деформация упругого последействия разгруженного бетона; - остаточная деформация из-за необратимого сплющивания пустот и излома их стенок (рис. 1).

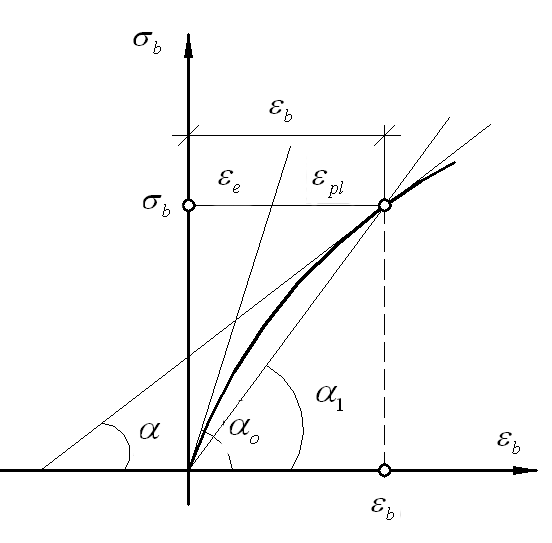
Рис. 1.

Начальный модуль упругости равен:

Секущий модуль упругости:

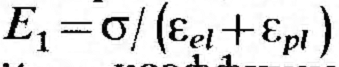
8. Распределение напряжений в изгибаемом элементе. Механизм разрушения.

РасПри совместном действии изгибающего момента М и поперечной силы Q распределение напряжений в нормальных сечениях элементов носит сложный характер (рис. 1).

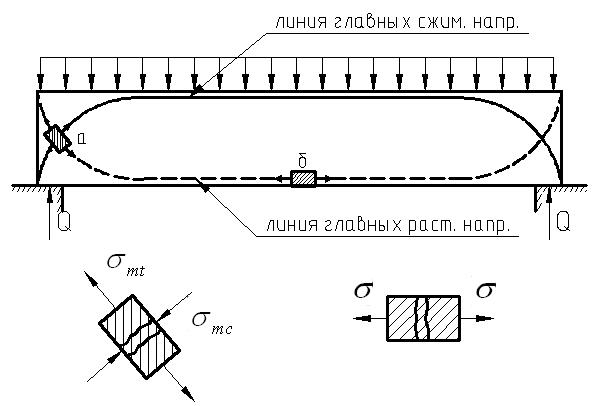
Рис. 1.

Механизм разрушения железобетонных элементов по наклонному сечению. При поперечном изгибе элемента вследствие совместного действия вблизи опор изгибающего момента и поперечной силы возникают главные сжимающие и главные растягивающие напряжения (рис. 1). Когда главные растягивающие напряжения достигают прочности бетона на растяжение, в нем образуются наклонные трещины, которые разделяют элемент на два блока, соединенных между собой бетоном в сжатой зоне над трещиной, а также продольной и поперечной арматурой, пересекающей трещину (рис. 2).

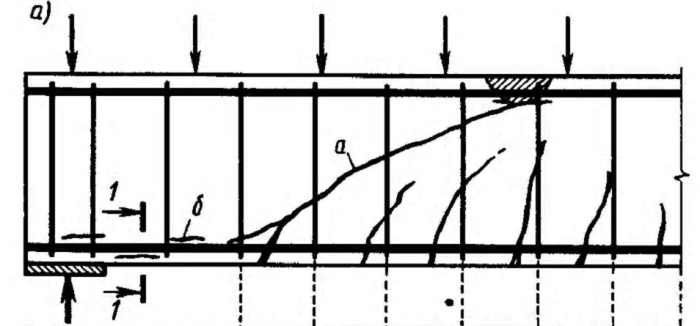
Рис. 2.

В этих условиях арматура работает на растяжение, а бетон над трещиной - на сжатие. С повышением нагрузки напряжения в поперечной и продольной арматуре, а также бетоне над наклонной трещиной возрастают. В зависимости от того, где напряжения быстрее достигнут предельных значений, различают три случая разрушения элемента по наклонным сечениям.

Случай 1 – разрушение по наклонной полосе между наклонными трещинами.

Главные сжимающие напряжения в бетоне между наклонными трещинами достигают предела прочности. В зоне действия поперечной силы происходит раздробление бетона и разрушение элемента.

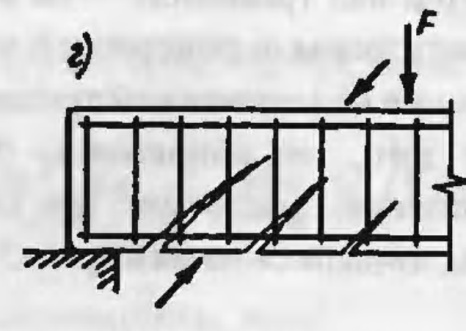
Рис. 3.

Случай 2 – разрушение по наклонной трещине в результате действия поперечной силы.

Напряжения только в поперечной арматуре, пересекающей наклонную трещину, достигают предела текучести. От действия преимущественно поперечной силы происходит срез бетона сжатой зоны над трещиной.

Обе части элемента при этом смещаются относительно друг друга. Такое разрушение возможно при наличии достаточно мощной и надежно заанкеренной продольной растянутой арматуры, препятствующей повороту обеих частей (рис. 4).

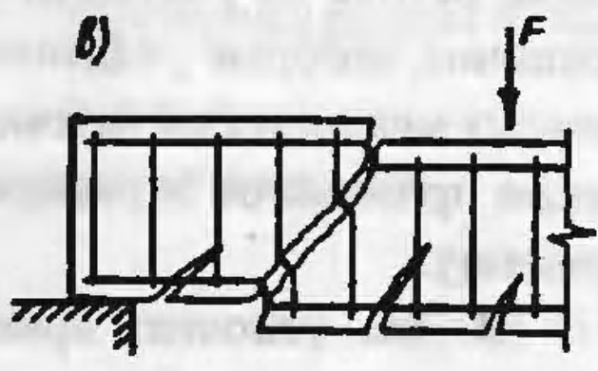
Рис. 4.

Случай 3 – разрушение в результате действия изгибающего момента.

Напряжения в продольной и поперечной арматуре, пересекаемой трещиной, достигают предела текучести. От действия изгибающего момента происходит взаимный поворот двух частей элемента относительно центра тяжести сжатой зоны бетона над трещиной (точка 0), до раздробления бетона (аналогично разрушению в нормальном сечении) (рис. 5).

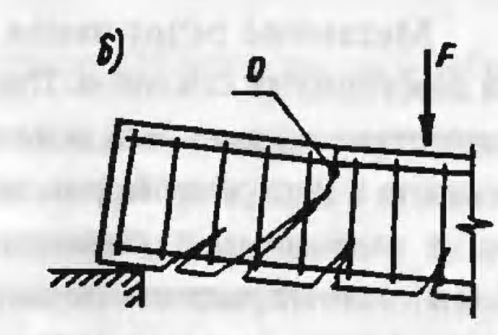
Рис. 5.