9. Адсорбция газов и паров.

Адсорбционные процессы изучают по кривым адсорбции, устанавливающим зависимость между тремя основными величинами: количеством поглощаемого газа (Q); равновесным давлением (Р); температурой (Т).

Различают три основных типа кривых: изотерма α = F(P), при Т = const, изобара α = F(Т), при Р =const, изостера Р = F(Т), при α = const.

Чаще всего используются изотермы.

При выводе уравнения изотермы многослойной, полимолекулярной адсорбции принимают следующие допущения: 1) теплота адсорбции в первом слое постоянная и не зависит от количества поглощенного газа; 2) теплота адсорбции во втором и всех последующих слоях равна теплоте конденсации; 3) значение вероятности конденсации и минимальное время адсорбции одинаковы для всех адсорбционных слоев.

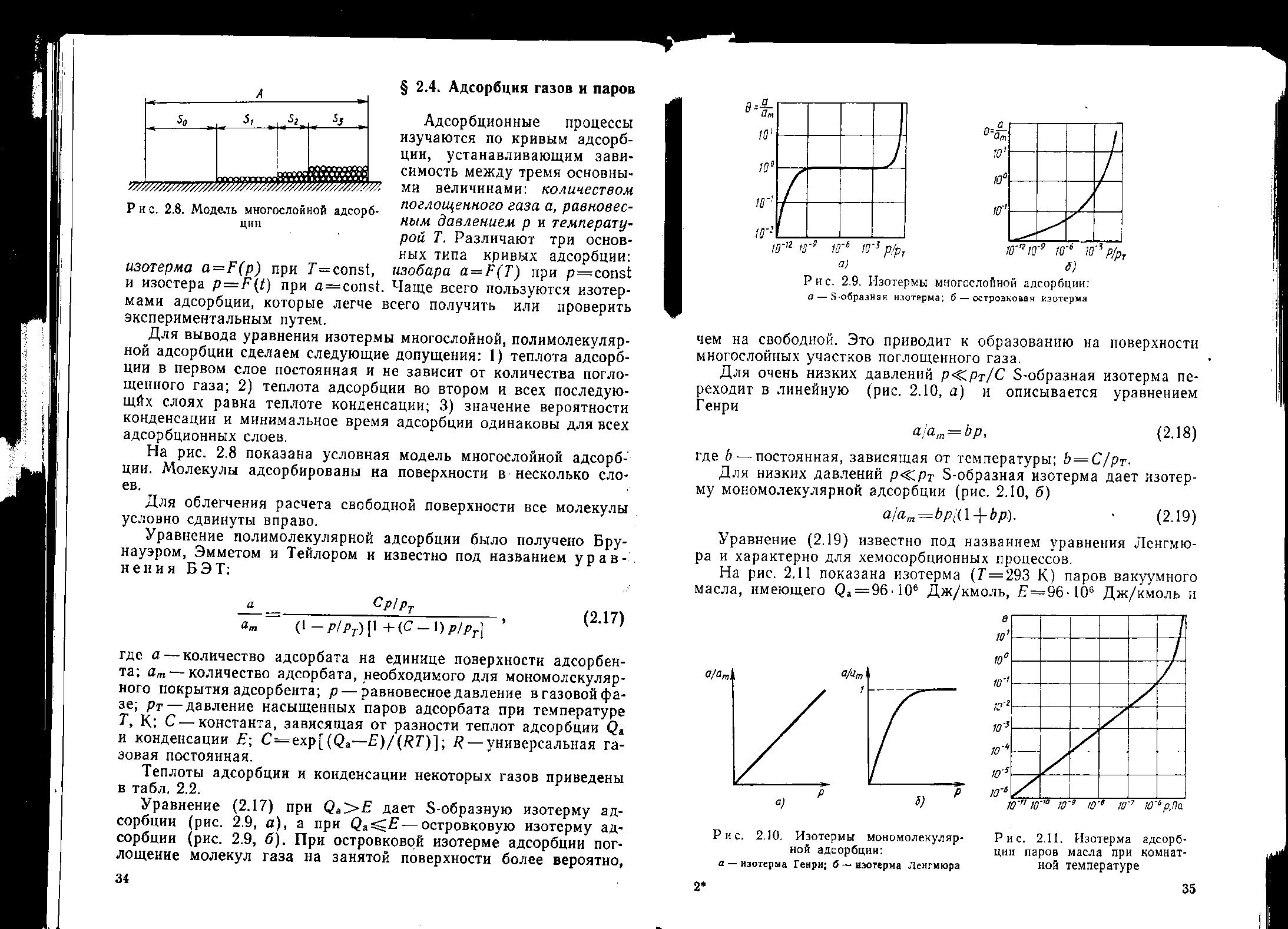
Рис. 2.2. Условная модель многослойной адсорбции.

Для облегчения расчета свободной поверхности все молекулы условно сдвинуты вправо, молекулы адсорбированы на поверхности в несколько слоев (рис.2.2).

Уравнение полимолекулярной адсорбции было получено Брунауэром, Эмметом и Тейлором и известно под названием уравнения БЭТ:

, (2.14)

где а – количество адсорбата на единице поверхности адсорбента; а_т – количество адсорбата, необходимого для мономолекулярного покрытия адсорбента; р – равновесное давление в газовой фазе; р_Т – давление насыщенных паров адсорбата при температуре Т, К; С – константа, зависящая от разности теплот адсорбции Q_a и конденсации Е; C=exp[(Q_a—E)/(RT)]; R – универсальная газовая постоянная.

При Q_a>E дает S-образную изотерму адсорбции, а при Q_a≤E – островковую изотерму адсорбции.

При островковой изотерме адсорбции поглощение молекул газа на занятой поверхности более вероятно, чем на свободной. Это приводит к образованию на поверхности многослойных участков поглощенного газа.

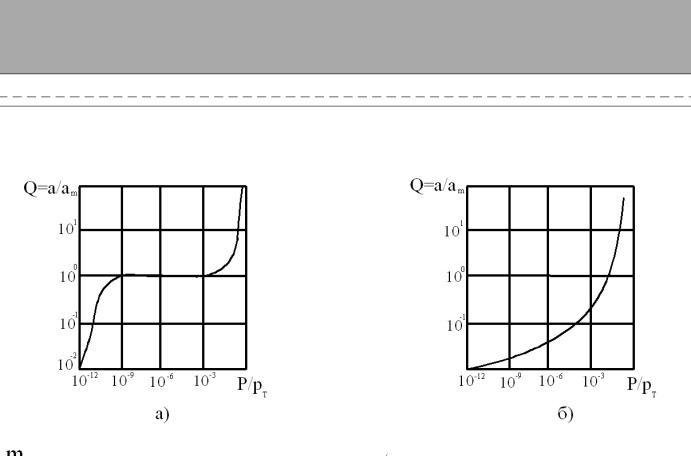
Рис.2.3. Изотермы многослойной адсорбции:

а) S – образная изотерма; б) островковая изотерма

Для очень низких давлений S-образная изотерма переходит в линейную и описывается уравнением Генри

, (2.15)

где b — постоянная, зависящая от температуры; b=C/p_T.

Для низких давлений S-образная изотерма дает изотерму мономоле-кулярной адсорбции.

. (2.16)

Уравнение (2.16) известно под названием уравнения Ленгмюра и характерно для хемосорбционных процессов.

Рис. 2.4. Изотермы мономолекулярной адсорбции:

а) изотерма Генри; б) изотерма Ленгмюра

Уравнение (2.14) при a = G/A можно преобразовать к виду

, (2.17)

где G – общее количество адсорбированного газа; А – полная поверхность адсорбента.

Обрабатывая экспериментальные данные G=f(p) в координатах и , относительно которых записанное уравнение линейно, можно найти две константы: А и С, а константа С позволяет по известной теплоте конденсации рассчитать теплоту адсорбции.

9. Степени покрытий поверхности.

Степень покрытия поверхности молекулами адсорбированных газов влияет на характер протекания поверхностных явлений: эмиссию электронов из твердого тела, поверхностный электрический разряд, сухое трение и износ, адгезию пленок и т. д.

Устанавливают три степени покрытия поверхности: высокую (θ»1), среднюю (θ ≈1) и низкую (θ «1). Для расчета равновесных значений θ можно воспользоваться уравнением (2.14), позволяющим рассчитывать θ при любых степенях покрытия.

В тех случаях, когда время установления адсорбционного равновесия мало, θ не будут достигать равновесных значений. Для определения влияния времени установления адсорбционного равновесия на долю поверхности, покрытой слоем адсорбированных молекул, необходимо решить дифференциальное уравнение адсорбции на гладкой поверхности. Для случая мономолекулярной адсорбции оно может быть записано в следующем виде:

, (2.18)

где – удельная скорость адсорбции; – удельная скорость конденсации на свободной поверхности; – удельная скорость испарения с поверхности, покрытой мономолекулярным адсорбционным слоем.

Если принять за равновесное состояние α = 0,99 α_∞, то время достижения сорбционного равновесия при начальном условии Q_о = 0.

. (2.19)

При адсорбции азота на графите для р = 1,33·10⁴ Па; Т = 293 К; а_m = 9,6.10¹⁸ м^-2; f = l; τ₀=10^-13с получим t_Р=3×10^-11с, что говорит о том, что при высоких давлениях или температурах адсорбционное равновесие устанавливается практически мгновенно.

При низких давлениях или температурах адсорбционное равновесие устанавливается достаточно медленно. Так, для паров масла (М = 422 кг/кмоль) при р=1,3·10⁹Па; Т=298 К; Qa = 96·10⁶ Дж/кмоль; а_m=6,67·10¹⁷ 1/м² получим t_Р ≈ 10⁵ с, т. е. величину, соизмеримую с временем эксперимента.