4. Газовые законы.

Если в объеме находится смесь из К газов, то давление смеси:

(1.8)

или (1.9) – закон Дальтона.

Т. к. температура, согласно 4 постулату, пропорциональна кинетической энергии молекулы, можно записать ,

где с – некоторая постоянная.

Тогда (1.7) можно записать в виде:

.

Обозначим , тогда (1.10),

а средняя кинетическая энергия молекулы:

(1.11)

Уравнение (1.10) называют уравнением газового состояния, оно связывает три основных параметра: давление, молекулярную концентрацию и температуру. Константа k=1.38∙10^-23Дж/к – постоянная Больцмана.

Уравнение (1.10) также можно представить в виде:

, (1.12),

где М – молекулярная масса газа; V – объём газа; N_A=М/m=6.02∙10²⁸ к моль^-1 – число Авагадро; R=kN_A=8.31∙10³, Дж/Кмоль – универсальная газовая постоянная.

5. Частота соударений молекул газа с поверхностью. Единицы давления.

Число молекул, соударяющихся об единицу поверхности в единицу времени:

(1.13)

С учетом функции распределения молекул по скоростям получаем

, (1.14)

где V_ар – средняя арифметическая скорость.

Объем газа, ударяющегося об единицу поверхности в единицу времени можно выразить через частоту соударений и молекулярную концентрацию

(1.15)

Данное выражение не зависит от давления и определяет максимальную быстроту действия идеального вакуумного насоса, откачивающего все молекулы газа, которые попадают в него через входное отверстие.

6. Распределение молекул газа по скоростям.

При соударении друг с другом или со стенками вакуумной камеры молекулы изменяют свои скорости, как по величине, так и по направлению. Используя гипотезы о стационарном распределении по скоростям и изотропности пространства, Максвелл получил функцию распределения молекул по скоростям

, (1.16)

где dn_V – число молекул скорости, которых находятся в пределах от V до 0.

Скорость, при которой наблюдаются максимальные функции распределения, называют наиболее вероятной скоростью

. (1.17)

Если ввести обозначения , то получим .

Используются безразмерная дифференциальная – f(c)=dn_V/(ndc) b и интегральная – F(c)= функции распределения молекул по скоростям.

В расчетах также используют среднеарифметическую скорость

(1.18)

и среднеквадратичную

(1.19).

Соотношение между скоростями V_вер, V_ар, V_кв составляет 1:1,128:1,225.

Кроме распределения по скоростям молекул имеются функции распределения по энергии

;

; (1.20)

, (1.21),

здесь .

Существуют наиболее вероятная энергия и среднеарифметическая .

7. Средняя длина свободного пути.

Направленный молекулярный поток, содержащий в начальный момент N₀ молекул газа с хаотично движущимися молекулами с частотой К за время dt, уменьшается на величину:

, интегрируя, получаем .

(1.22)

Средняя длина свободного пути молекул газа , определяемая как отношение скорости молекул к числу столкновений в единицу времени. – длина пути молекулы за время t, столкновение произойдет в том случае, если расстояние между центрами молекул будет не более диаметра молекулы . Будем считать, что одна молекула имеет радиус , а все остальные математические точки с нулевым радиусом. При движении со скоростью с молекулярной концентрацией n, за одну секунду такая воображаемая молекула опишет объем , и испытает столкновений. Средняя длина свободного пути в таком случае будет равна

. (1.23)

С учетом относительных скоростей движения молекулы газа, которые не учитывались при выводе уравнения (1.23), для длины свободного пути можно получить более точное выражение

. (1.24)

Из (1.24) видно, что при постоянной молекулярной концентрации, длина свободного пути не должна зависеть от температуры.

Однако из опытных данных следует, что при n = const, средняя длина свободного пути увеличивается , данный фактор учитывается введением дополнительного модуля, тогда

, (1.25)

где С – постоянная Сезерленда, равная температуре при которой, в случае постоянной молекулярной концентрации газа, средняя длина свободного пути молекул уменьшается вдвое по сравнению со значением соответствующей бесконечно большой температуре [K] .

Для учета взаимодействия молекул между собой вводят понятие эффективного диаметра молекулы dТ, который уменьшается с увеличением температуры

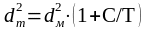(1.26)

Уравнение (1.25) с учетом (1.26) можно записать в виде:

.

Используя уравнение состояния (1.10), (1.26) можно записать в виде:

(1.27)

Для воздуха, при Т=293 К, и Р=1Па из (1.27), L₁= 6,7·10^-3 МПа.

L₁ – средняя длина свободного пути при Р=1Па.

При любом другом давлении

(1.28)

При расчетах длины свободного пути при различных температурах и постоянном давлении из (1.27) можно получить

(1.29)

В случаи смеси двух газов с массой молекул m₁ и m₂, L₁ молекулы массой m₁ рассчитывают по формуле:

; (1.30)

.

В случае, если n₁« n₂, получаем

. (1.31)

Формула Больцмана для определения давления воздуха на различной высоте z

.