
- •3. Репрезентативность.
- •5. Типологическая и структурная группировки
- •9. Характеристики центра распределения.Средняя арифметическая
- •10. Понятие медианы
- •12. Показатели вариации.
- •13. Абсолютные и относительные величины;
- •14. Ряды динамики.
- •15. Определение среднего уровня
- •16. Показатели динамики
- •17. Средний абсолютный прирос
- •18. Выделение тренда.
- •21. Линейная модель тренда,
- •22. Индексы и их применение
- •23. Общие (агрегатные) индексы
- •24. Взаимосвязь агрегатных и индивидуальных индексов. Вычисление агрегатных индексов по индивидуальным индексам
21. Линейная модель тренда,
осуществляется
подстановкой значения фактора
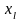 в оценку детерминированной составляющей:
в оценку детерминированной составляющей:
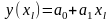 Чтобы
определить точность этой оценки и
построить доверительный интервал
необходимо найти дисперсию оценки
Чтобы
определить точность этой оценки и
построить доверительный интервал
необходимо найти дисперсию оценки
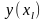 .
.
На практике для оценки дисперсии ошибки прогноза можно пользоваться следующим выражением
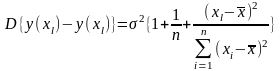 .
.
Из
этого выражения следует, что с ростом
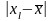 дисперсия
ошибки прогноза увеличивается.
дисперсия
ошибки прогноза увеличивается.
22. Индексы и их применение
Индивидуальные индексы
В статистике под индексом понимают относительную величину, характеризующую результат сравнения двух уровней одноименных показателей.
Каждый индекс включает два вида данных: данные текущего (отчетного) периода и данные базисного периода, служащие базой для сравнения.
Различают индивидуальные и общие (агрегатные) индексы.
Индивидуальные индексы характеризуют изменение отдельных элементов статистической совокупности
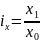
где
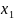 - текущий уровень величины;
- текущий уровень величины;
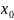 -
базисный уровень величины.
-
базисный уровень величины.
Различают индексы абсолютных показателей (объема продукции, товароооборота и т. д.) и относительных показателей (цен, себестоимости и т. д.).
Общие (агрегатные) индексы
Общие (агрегатные) индексы строятся с учетом изменения всех элементов статистической совокупности.
А) Агрегатный индекс товарооборота
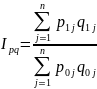
где n- количество товаров;
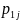 ,
,
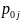 - цена j-го
товара в текущем и базовом периодах
соответственно;
- цена j-го
товара в текущем и базовом периодах
соответственно;
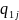 ,
,
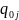 - количество j-го
товара в текущем и базовом периодах
соответственно.
- количество j-го
товара в текущем и базовом периодах
соответственно.
Б) Агрегатный индекс цен
Так как совокупность состоит из элементов, непосредственно не поддающихся суммированию, то агрегатный индекс включает набор значений цен и соответствующих им весовых коэффициентов
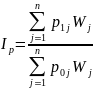
При
этом возникает вопрос что использовать
в качестве весов
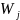 .
В экономическом анализе приняты два
варианта.
.
В экономическом анализе приняты два
варианта.
В первом варианте в качестве весов принимается физический объем производства текущего периода (индекс Пааше)
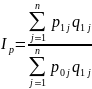
Во втором варианте в качестве весов принимается физический объем производства базисного периода (индекс Ласпейреса)
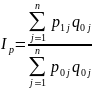
Обычно на практике используется индекс Пааше.
В) Индекс физического объема
Индекс физического объема использует в качестве весов цены базисного периода
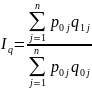
Тогда индекс товарооборота будет равен
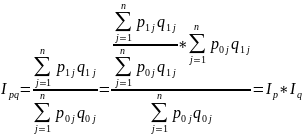
23. Общие (агрегатные) индексы
Общие (агрегатные) индексы
Общие (агрегатные) индексы строятся с учетом изменения всех элементов статистической совокупности.
А) Агрегатный индекс товарооборота
где n- количество товаров;
, - цена j-го товара в текущем и базовом периодах соответственно;
, - количество j-го товара в текущем и базовом периодах соответственно.
Б) Агрегатный индекс цен
Так как совокупность состоит из элементов, непосредственно не поддающихся суммированию, то агрегатный индекс включает набор значений цен и соответствующих им весовых коэффициентов
При этом возникает вопрос что использовать в качестве весов . В экономическом анализе приняты два варианта.
В первом варианте в качестве весов принимается физический объем производства текущего периода (индекс Пааше)
Во втором варианте в качестве весов принимается физический объем производства базисного периода (индекс Ласпейреса)
Обычно на практике используется индекс Пааше.
В) Индекс физического объема
Индекс физического объема использует в качестве весов цены базисного периода
Тогда индекс товарооборота будет равен
агрегатных и индивидуальных индексов
Агрегатный индекс связан с индивидуальными индексами . При этом агрегатный индекс является некоторой средней из индивидуальных индексов с соответствующими весами.
Предположим,
что известны индивидуальные индексы
цен
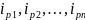 .
.
Тогда
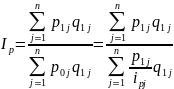
Данная
формула представляет собой средневзвешенное
гармоническое из индивидуальных
индексов цен с весами
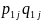 .
.
Предположим,
что известны индивидуальные индексы
физического объема
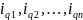 .
.
Тогда
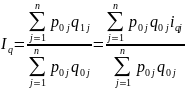
Данная
формула представляет собой средневзвешенное
арифметическое из индивидуальных
индексов физических объемов с весами
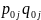 .
.
