1 вопрос

Основными кинематическими характеристиками движущейся точки являются её скорость и ускорение, значения которых определяются по уравнениям движения через первые и вторые производные по времени от s или от х, у, z, или от r. Способы задания движения твёрдого тела зависят от вида, а число уравнений движения — от числа степеней свободы тела. Простейшими являются Поступательное движение и Вращательное движение твёрдого тела. При поступательном движении все точки тела движутся одинаково, и его движение задаётся и изучается так же, как движение одной точки. При вращательном движении вокруг неподвижной оси z (рис. 3) тело имеет одну степень свободы; его положение определяется углом поворота φ, а закон движения задаётся уравнением φ = f (t). Основными кинематическими характеристиками являются угловая скорость ω=dφ/dt и угловое ускорение ε = dω/dt тела. Величины ω и ε изображаются в виде векторов, направленных вдоль оси вращения. Зная ω и ε, можно определить скорость и ускорение любой точки тела.

2 Вопрос

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ὠ и угловое ускорение ε.

Вращательное движение тела вокруг неподвижной оси характеризуется тем, что любые точки тела описывают окружности, лежащие в параллельных плоскостях, а центры этих окружностей лежат на одной прямой, называемой осью вращения.

При вращательном движении инерция тела зависит не только от массы, но и от распределения ее в пространстве относительно оси вращения. Чем дальше от оси вращения распределена масса тела, тем больше ее инерция.

Мерой инертности тела при вращении является физическая величина, называемая моментом инерции тела относительно оси.

3 Вопрос

Связь между линейной и угловой скоростями  , между линейным и угловым ускорениями вращающейся точки твердого тела  .

При разложении вращательного движения на нормальное и касательное направления ускорения имеют вид:

4 Вопрос

Масса - основная динамическая характеристика тела , количественная мера его инертности , т . е . способности тела приобретать определённое ускорение под действием силы . Для данного тела ускорение пропорционально силе , и коэффициентом пропорциональности является масса . Единица массы в СИ - 1 Кг .

Импульс - векторная величина , имеет такое же направление , что и скорость. Единица импульса в системе СИ = 1 кг • 1 м/c .

Используя второй закон Ньютона можно вычислить массу тела , измерив независимо силу и ускорение .

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.

Второй закон Ньютона: ускорение тела прямо пропорционально вызывающей его силе и обратно пропорционально массе тела:

.

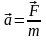Если на тело действует несколько сил, то во втором законе Ньютона под понимают равнодействующую силу.

5 Вопрос

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.

6 Вопрос

Инертные свойства тела при вращательном движении характеризует момент инерции. Он зависит от распределения массы тела относительно оси вращения. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси:  .

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласнотеореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, используют теорему Штейнера: момент инерции тела I относительно некоторой оси равен сумме момента инерции тела I₀ относительно параллельной оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями d.