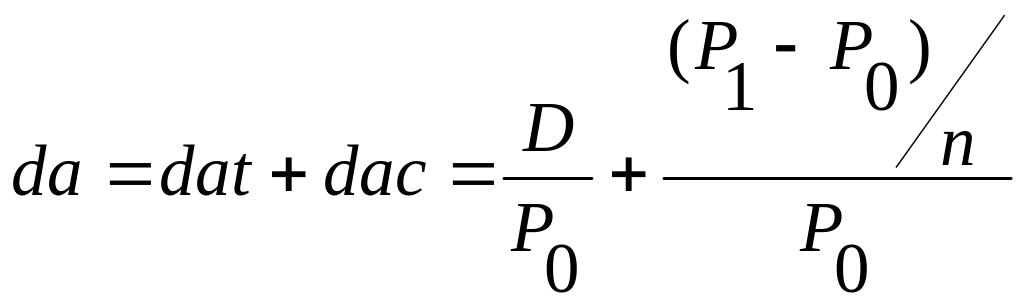2.5.3. Доходность акции

По аналогии с облигациями формулы, рассмотренные в разделе (2.2), посвященном оценке акций, могут применяться и для оценки значений ожидаемой доходности акций; при этом в соответствующих формулах необходимо лишь заменить теоретическую стоимость V, на ры­ночную цену Р. Таким образом, доходность бессрочной привилеги­рованной акции, равно как и обыкновенной акции с неизменным дивидендом, находится по формуле

(2.5.7)

где da – доходность акции;

D – ожидаемый дивиденд;

P – текущая рыночная цена акции.

В формуле (2.5.7) общая доходность акции совпадает с текущей дивидендной доходностью. Эту формулу можно применять, если после покупки акции инвестор не предполагает продать ее в бли­жайшем будущем.

Если инвестор приобретает акцию в спекулятивных целях, намереваясь продать ее через некоторое время, то он может получить некоторые оценки ожидаемых значений общей, дивидендной и капитализированной доходности, пользуясь формулой (2.5.2):

(2.5.8)

где da – доходность акции;

dat – текущая (дивидендная) доходность акции;

dac – капитализированная доходность акции;

– рыночная цена акции на момент принятия решения о покупке;

– ожидаемая цена акции на момент ее предполагаемой продажи;

– ожидаемое число лет владения акцией.

Оценка ожидаемой доходности конвертируемой привилегированной акции также может быть получена с помощью формулы (2.5.8), в которой в качестве P1 следует использовать ожидаемую конверсионную стоимость акции.

Для оценки значений ожидаемой общей доходности обыкновенных акций с равномерно возрастающими дивидендами можно воспользоваться формулой (2.2.8):

(2.5.9)

где da – доходность акции;

dat – текущая (дивидендная) доходность акции;

dac – капитализированная доходность акции;

– последний полученный к моменту оценки дивиденд по акции;

– ожидаемый дивиденд;

– цена акции на момент оценки;

– темп прироста дивиденда.

Из формулы (2.5.9) видно, что ожидаемая капитализированная доходность обыкновенной акции с равномерно возрастающим дивидендом совпадает с темпом прироста дивиденда или с темпом прироста цены акции. Таким образом, показатель g имеет несколько интерпретаций: во-первых, это капитализированная доходность; во-вторых, темп прироста дивиденда; в-третьих, темп прироста цены акции.

2.5.4. Оценка риска финансовых активов

Концепция учета фактора риска в финансовой деятельности состоит в объективной оцен­ке его уровня с целью обеспечения формирования необходимого уровня доходности финансовых операций и разработки системы мероприятий, минимизирующих его негативные финансовые по­следствия для хозяйственной деятельности предприятия.

Капитальные финансовые активы условно делятся на две группы: рисковые и безрисковые. Рисковость актива характеризуется сте­пенью вариабельности дохода (или доходности), который может быть получен благодаря владению данным активом.

По безрисковому финансовому активу доход предопределен (не меняется в зависимости от действия каких-либо рыночных фак­торов). К безрисковым активам можно отнести го­сударственные ценные бумаги (например, облигации). Безрисковые финансовые операции — финансовые операции, по которым отсутствует реальный риск потери капитала или дохода и гарантировано получение расчетной реальной суммы прибыли.

Финансовый актив, ожи­даемые доходы по которому заранее точно не известны (не могут быть спрогнозированы с абсо­лютной точностью), является рисковым. К рисковым активам можно отнести корпоративные ценные бумаги (обыкновенные акции, облигации и др.) по­скольку доход по такого рода активам может ощутимо варьировать.

Активы, с которыми ассоциируется относительно больший размер возможных потерь, рассматриваются как более рисковые; вполне есте­ственно, что к таким активам предъявляются и большие требования в отношении доходности.

Количественно риск финансового актива может оцениваться вариабельностью доходности (не дохода), мерой которой выступают дисперсия (ф. 2.3.1.) и среднее квадратическое отклонение (ф. 2.3.2). В связи с тем, что доходность относительный показатель, рассчитывать коэффициент вариации нет необходимости. Чем больше дисперсия (среднеквадратическое отклонение), тем выше риск.

В перспективном анализе риска инвестор сталкивается с проблемой оценки ожидаемых значений доходности и их вероятностей. Обычно применяют три оценки: пессимистическую (dp), наиболее вероятную (dr) и оптимистическую (do). В этом случае наиболее общей мерой риска, ассоциируемого с данным активом, может служить размах вариации ожидаемой доходности, рассчитываемый по формуле

(2.5.10)

Риск, ассоциируемый с определенным активом, как правило, рассматривают во времени. Очевидно, чем дальше горизонт планирования, тем труднее предсказать доходность актива, и, соответственно, размах вариации доходности, равно как и дисперсия и коэффициент вариации, увеличивается. Таким образом, с течением времени риск, ассоциируемый с данным активом, возрастает. Отсюда можно сделать очень важный вывод: чем более долговременным является данный вид актива, тем он более рискован, тем большая вариация доходности с ним связана, Именно поэтому различаются доходность и рисковость различных финансовых инструментов, например акций и облигаций: вариация доходности акций может ощутимо варьировать, т.е. этот вид финансового инструмента более рискован.

Одним из важнейших показателей рисковости финансовых активов является -коэффициент. Бета-коэффициент характеризует уровень изменчивости курса котировки отдельного финансового инструмента (ценной бумаги) или их портфеля по отношению к динамике сводного индекса цен всего финансового (фондового) рынка. Бета-коэффициент является показателем систематического (или недиверсифицированного) риска.

Систематический (рыночный) риск — риск, связанный с изменением конъюнктуры всего финансового рынка (или отдель­ных его сегментов) под влиянием макроэкономических факто­ров. Он возникает для всех участников этого рынка и не может быть устранен ими в индивидуальном порядке. Чем выше значение бета-коэффициента, тем выше уровень систематичес­кого и общего риска по конкретному финансовому инструменту или их портфелю в целом.

Этот показатель используется обычно для оценки рисков инвестирования в отдельные ценные бумаги. Расчет этого показателя осуществляется по формуле:

(2.5.11)

где  — бета-коэффициент;

k — коэффициент корреляции между уровнем доходности по инди­видуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;

и — среднеквадратическое отклонение доход­ности по индивидуальному виду ценных бумаг (или по их портфелю в целом);

р — среднеквадратическое отклонение доходности по фондовому рынку в целом.

Уровень финансового риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициента:

 = 1 — средний уровень;

 > 1 — высокий уровень;

 < 1 — низкий уровень.

Оценивая риск конкретного актива, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой частью портфеля. Оценки риска в этих двух вариантах могут существенно различаться. Актив, имеющий высокий уровень риска при рассмотрении его изолированно, может оказаться практически безрисковым с позиции портфеля и при определенном сочетании входящих в этот портфель активов. Поэтому чаще всего инвестор работает не с отдельным активом, а с некоторым их набором, называемым портфелем ценных бумаг, или инвестиционным портфелем.