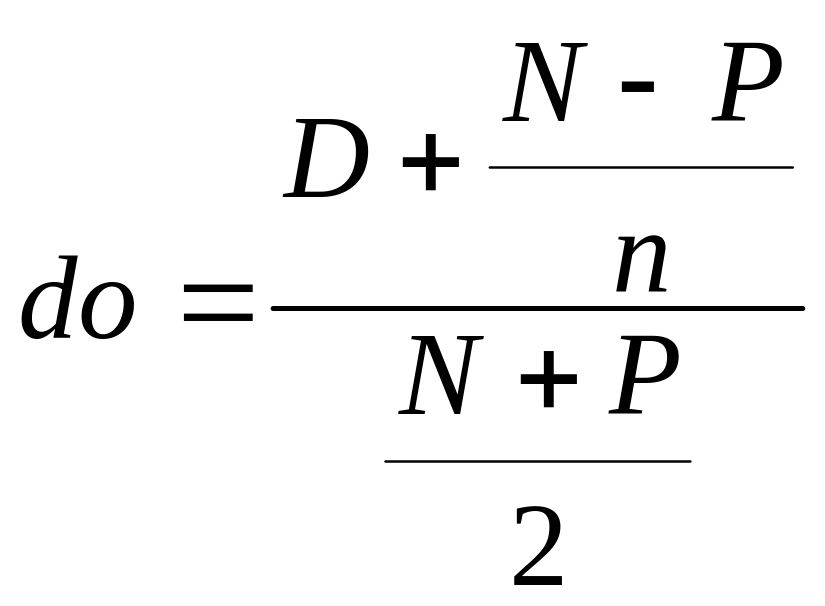2.5. Риск и доходность финансовых активов

2.5.1. Понятие и измерение доходности финансового актива

Риск и доходность в финансовом менеджменте рассматриваются как две взаимосвязанные категории. Они могут быть ассоциированы и с каким-либо отдельным видом финансовых активов, и с их комбинацией. Одной из базовых концепций финансового менеджмента является положение об однонаправленности изменения риска и доходности: чем выше ожидаемая доходность, тем выше риск вложений в соответствующие финансовые активы. И наоборот, к активам, с которыми ассоциируется относительно больший размер возможных потерь, предъявляются и большие требования в отношении доходности.

Следует различать доход и доходность. Доход – абсолютный показатель, доходность – относительный. В зависимости от вида финансового актива в качестве дохода о чаще всего выступают дивиденд, процент, прирост капитализирован­ной стоимости. В разделе 2.2 были рассмотрены абсолютные показате­ли и возможности их использования в ситуациях, когда необходимо принять решение о целесообразности приобретения финансовых активов. Доходность актива (d) – это показатель, рассчитываемый соотнесением до­хода (D), генерируемого данным финансовым активом, и величины ин­вестиции (1) в этот актив:

d = D / I.

(2.5.1)

Доходность, исчисленная в процентах, по существу представляет собой рентабельность данного актива или норму прибыли, однако традиционно термин «рентабельность» используется по отношению к материальным активам, а термин «доходность» по отношению к финансовым активам и капиталу.

В финансовых расчетах доход, обеспечиваемый каким-либо активом, обычно разделяют на две составляющих: 1) регулярные выплаты владельцу актива, 2) рост стоимости самого актива. Соответственно ожидаемая доходность также будет складываться из двух составляющих – текущей и капитализированной доходности:

(2.5.2)

где d – доходность финансового актива;

Р0 – цена приобретения финансового актива (в начале рассматриваемого периода);

Р1 – цена финансового актива в конце периода (ожидаемая величина);

D1 – регулярные вылаты в предстоящем периоде (ожидаемая величина);

D1 + (P1 – Р0) – общий доход в предстоящем периоде;

dt – текущая доходность (в приложении к акциям она называется также дивидендной);

dc – капитализированная доходность.

Таким образом, выбирая для покупки финансовый актив, инвестор дол­жен расставить для себя приоритеты — что важнее, регулярный доход или прирост стоимости актива.

В рамках фундаменталистской теории возможен другой подход к расчету доходности. Логика рассуждений в этом случае такова: если известна теку­щая цена финансового актива и доходы, которые, как ожидает­ся, этот актив будет генерировать в будущем, то на основе формулы оценки настоящей стоимости денежного потока можно рассчитать параметр r, значение которого можно трактовать как доходность данного актива.

2.5.2. Доходность облигаций

Оценка стоимости облигации выполняется по формуле (2.2.13). Эта же формула может использоваться для оценки доходности облигации. В этом случае Vопд – текущая рыночная цена облигации – известна, а неизвестна величина r. Решение уравнения относительно г определяет доходность данной облигации. Этот показатель иногда называется доходностью к погашению и обозначается YTM (Yield to Maturity). В условиях эффективного рынка все облигации одного класса теоретически должны иметь примерно одинаковую до­ходность.

Для приблизительной оценки доходности купонной облига­ции без права досрочного погашения рассчитывается отношение среднегодового дохода (годовой процент плюс часть разницы между номинальной стоимостью и ценой покупки облигации) к средней величине инвес­тиции:

(2.5.3)

где do — доходность облигации;

N — номинал облигации;

Р — текущая цена (на момент оценки);

D — купонный доход;

n — число лет, оставшихся до погашения облигации.

Достоинством показателя do, как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе при выборе вариантов инвестирования в те или иные облигации. Формула (2.5.3) обеспечивает достаточную точность расчетов.

В некоторых отечественных пособиях по финансовому анализу для оценки эффективности инвестирования в облигации рекомендуют ориентироваться на показатель текущей, или дивидендной, доходности, под которым понимается отношение дохода, получаемого ежегодно по купонной ставке, к фактическим затратам на приобретение облигации:

(2.5.4)

где dot – текущая доходность облигации;

N – номинальная стоимость облигации;

P – текущая рыночная стоимость облигации;

k – купонная ставка.

Из формулы (2.5.4) видно, что показатель текущей доходности не может использоваться в качестве обобщенной характеристики и кри­терия при анализе целесообразности инвестирования в данные об­лигации. Он дает искаженную оценку доход­ности облигации, поскольку не учтитывает доход ее держа­теля, полученный от приобретения облигации с дисконтом.

Еще одной характеристикой доходности облигации явля­ется показатель купонной доходности, рассчитываемый по следую­щей формуле:

(2.5.5)

Чаще всего этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходнос­ти облигации невысока, а именно: эта ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она использует­ся в основном для расчета купонного дохода.

Облигации с правом досрочного погашения имеют, кроме рассмотренных, еще одну характери­стику — доходность досрочного погашения (Yield to Call, YTC). Этот показатель дает оценку доходности на момент отзыва облигации с рынка, или ее досрочного погашения. По аналогии с общей доходнос­тью показатель YTC находится из формулы (2.2.13), в которой номинал N заменен выкупной ценой Р.

Конвертируемая облигация предусматривает при выполнении не­которых условий возможность ее обмена на n-е число обыкновенных акций эмитента. Обмен может осуществляться, например, на основа­нии коэффициента конверсии rс. В этом случае облигация имеет так называемую конверсионную стоимость (Рс), которая связана с рыноч­ной ценой базисного актива (обыкновенной акции) Рs следующим соотношением:

(2.5.6)

Оценка ожидаемой доходности конвертируемой облигации находится из формулы (2.2.13), в которой номинал N заменен ожидаемой конверсионной стоимостью. Основным моментом в процессе анализа является установление прогнозной оценки стоимости базисного актива на тот или иной момент времени.