30. Закон Джоуля-Ленца. Формулы для вычисления мощности, выделяющейся на сопротивлении.
Закон Джоуля – Ленца: «Если по проводнику протекает ток, в проводнике выделяется теплота Q».
Мощность, выделяющаяся на сопротивлении
нагрузки, является полезной мощностью
источника тока, по закону Джоуля-Ленца
она равна
.
Мощность, выделяющаяся на внутреннем
сопротивлении, представляет собой
тепловые потери на нагревание
источника, полная мощность выделяется
на суммарном сопротивлении всей цепи:
.
|
закон Джоуля - Ленца в интегральной форме |
при постоянной силе тока, R – общее сопротивление участка цепи |
|
для случая, когда сила тока зависит от времени |
31. Закон Джоуля-Ленца в локальной (дифференциальной) форме.
|
(17.13) |
Соотношение (17.13)
выражает закон Джоуля-Ленца в интегральной
форме. Введем плотность тепловой
мощности 
,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
где S - поперечное
сечение проводника, 
-
его длина. Используя (1.13) и соотношение 
,
получим
Но 
-
плотность тока, а 
,
тогда
с учетом закона
Ома в дифференциальной форме 
,
окончательно получаем
|
(17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
32. Электрическое сопротивление при параллельном и последовательном соединении проводников.
сопротивление цепи,
состоящей из нескольких последовательно
соединенных участков,
равно сумме сопротивлений
каждого участка
при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R - сопротивление проводника, 1/R - электрическая проводимость проводника)
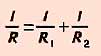Если
в цепь включены параллельно только два
сопротивления, то:
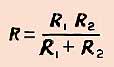
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
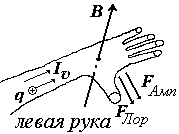
33.Сила Лоренца (в векторной и скалярной формах). Вектор магнитной индукции, его размерность.
Неподвижные в некоторой системе отсчета К электрические заряды взаимодействуют между собой с кулоновской (электростатической) силой. Если эти заряды рассматривать, находясь в другой системе отсчета К, движущейся относительно системы К с постоянной скоростью v, и использовать формулы релятивистской механики, то выражение для силы взаимодействия зарядов оказывается другим.7 Появляется дополнительная сила, зависящая от скорости. Эту дополнительную силу называют магнитной силой. Кулоновская сила зависит от расстояния между зарядами, магнитная сила зависит от скорости движения зарядов. Полную силу взаимодействия зарядов называют силой Лоренца или электромагнитной силой.
|
сила Лоренца (электромагнитная сила); Е- напряженность электрического поля, В – индукция магнитного поля. |
Если электрический заряд движется, вокруг него, а также вокруг проводника с током (ток – это движущиеся направленно заряды) возникает поле, которое называют магнитным полем и характеризуют вектором В вектором магнитной индукции. Физический смысл вектора В можно определить из выражений для магнитных сил.
|
магнитная составляющая силы Лоренца действует на заряд, движущийся в магнитном поле; направлена всегда плоскости, в которой лежат v и В. |
|
|
сила Ампера действует на проводник dl с током I в магнитном поле; всегда направлена плоскости, в которой лежат dl и В |
()
()Из формулы (): B= Fmax/(qv) магнитная индукция численно равна максимальной силе, действующей на единичный положительный заряд, движущийся в магнитном поле с единичной скоростью ((sin)max=1). Из формулы (): B=Fmax/Il магнитная индукция численно равна максимальной силе, действующей в магнитном поле на проводник единичной длины, по которому течет единичный ток. Таким образом, вектор магнитной индукции – это силовая характеристика магнитного поля.