28. Закон Ома в локальной (дифференциальной) форме. Удельное сопротивление и удельная проводимость.

В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока   и вектор напряженности поля   коллинеарны.    Исходя из закона Ома имеем:

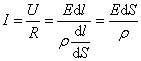
 А мы знаем, что   или  . Отсюда можно записать

это запись закона Ома в дифференциальной форме.

Здесь   – удельная электропроводность.

 (Ом.м)- удельное сопротивление – это характеристика электрических свойств металла, оно зависит от природы металла и от его температуры. По смыслу  - это электрическое сопротивление единицы длины проводника с единичной площадью поперечного сечения. С увеличением температуры сопротивление металлов увеличивается. При умеренных температурах удельное сопротивление линейно зависит от температуры:

(1/К)

зависимость удельного сопротивления металлов от температуры; 0 – удельное сопротивление при 0оС,  - температурный коэффициент сопротивления, определяющий относительное изменение сопротивления при нагревании проводника на один градус.

Удельная проводимость  - это мера способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде

29.Электронная(классическая) теория электропроводности металлов. Основные предположения теории и вывод закона Ома в локальной(дифференциальной) форме.

В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока   и вектор напряженности поля   коллинеарны.    Исходя из закона Ома имеем:

 А мы знаем, что   или  . Отсюда можно записать

это запись закона Ома в дифференциальной форме.

Здесь   – удельная электропроводность.

 (Ом.м)- удельное сопротивление

В рамках элементарной кинетической теории полагаем, что валентные электроны (электроны проводимости) металлов представляют собой одинаковые твердые сферы, двигаются они по прямым линиям до столкновения друг с другом, время контакта частиц пренебрежимо мало по сравнению с временем "свободного" движения.

      Объемную концентрацию электронов проводимости можно оценить выражением:

     

     где   - объемная плотность металла (кг/м³), Z - валентность химического элемента, N_a - число Авогадро, А - относительная атомная масса элемента.

      Заряд электрона е =-1,6*10^-19 Кл, масса электрона m_e = 0,91*10^-30 кг. Величину "е" ниже будем считать положительной, а знак заряда электрона будем учитывать непосредственно в формулах.

      Плотность электронного газа:

     

     значительно больше плотности обычных газов при нормальных условиях.