22. Энергия заряженного конденсатора.

Рассмотрим две параллельные одинаковые незаряженные пластины, Мысленно перенесем с одной пластины на другую бесконечно малый заряд +dq. Для этого не требуется никакой работы, т.к. пластина пока не заряжена. После этого пластины окажутся разноименно заряженными, и между ними появится разность потенциалов . Для переноса следующей «порции» заряда уже требуется работа dА = dq = dq(q/C), где С – емкость конденсатора. Каждая новая «порция» заряда будет повышать заряд q на пластине, и все труднее будет переносить новые порции. Поэтому для вычисления полной работы следует проинтегрировать.

	работа, которую надо затратить, чтобы зарядить конденсатор зарядом q. А=W
	энергия заряженного конденсатора

23.Энергия электростатического поля. Объемная плотность энергии.

(Дж/м3)

объемная плотность энергии - по смыслу – это энергия, приходящаяся на единицу объема пространства.

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:

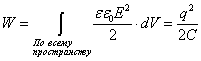
Энергия электростатического поля системы точечных зарядов равна: 

 

24.Энергия электростатического поля. Получите выражение для объемной плоскости энергии на примере плоского конденсатора.

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:

Энергия электростатического поля системы точечных зарядов равна: 

Получим формулы для энергии, выразив ее через характеристики электрического поля, существующего вокруг заряженных тел: напряженность Е и электрическую индукцию D. Рассмотрим плоский конденсатор, считая поле между обкладками однородным.

	энергия заряженного конденсатора
	 - разность потенциалов между обкладками, С -емкость плоского конденсатора, V – объем пространства между обкладками; подставим формулы в (), получим:
	электрическая энергия, сосредоточенная в пространстве между обкладками плоского конденсатора.

25. Сила тока. Плотность тока. Выражение для плотности тока через среднюю скорость носителей тока и их концентрацию.

	С ила тока (А = Кл/с) – скалярная величина, численно равна тому заряду, который проходит через поперечное сечение проводника за единицу времени. За направление силы тока традиционно принимается движение положительных зарядов 5.
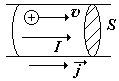
	Плотность тока (А/м2) – это вектор, направленный так же, как скорость движения положительных зарядов. Численно она равна силе тока, проходящего через единицу площади поперечного сечения или равна тому заряду, который проходит за единицу времени через единичное поперечное сечение проводника.

Получим формулу для плотности тока. Пусть в единице объема проводника длиной L, по которому течет ток, находится n носителей тока (электронов) с зарядом е. Средняя скорость направленного движения носителей v_ср .

	плотность тока (по определению)
	полный заряд, прошедший через сечение проводника за время t; N – число носителей тока в некотором объеме V проводника
	(1/м3) концентрация носителей тока, V – объем проводника
	средняя скорость направленного движения носителей (скорость дрейфа)

Подставив вышеприведенные формулы в первую из них, получим выражение, связывающее плотность тока с величиной заряда носителей тока (заряд электрона), их средней скорости направленного движения и концентрации.