19. Диполь и его электрический момент. Напряженность и потенциал поля диполя на его продольной оси. Расстояние от диполя много больше длины диполя.

Диполем называется система, состоящая из двух одинаковых по величине, но различных по знаку зарядов q, расположенных на определенном расстоянии l друг от друга. Если это расстояние не меняется, диполь называют жестким. Если расстояние меняется пропорционально напряженности внешнего поля, диполь называют упругим.

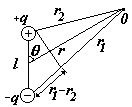
Диполь характеризуют дипольным (электрическим) моментом (см. рис.):

дипольный (электрический) момент диполя – это вектор, проведенный от отрицательного заряда к положительному

Для определения потенциала  и напряженности Е поля диполя можно воспользоваться принципом суперпозиции:

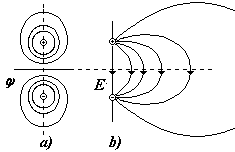
()	Электростатическое поле диполя имеет сложный вид (см. рис.): a) эквипотенциальные поверхности, b) силовые линии (половина поля)
- расстояния от точки поля 0, для которой определяются  и Е, до зарядов, - единичные векторы, взятые в этих направлениях (см. рис. ниже).

Из формулы () можно получить потенциал поля диполя для расстояний r, существенно превышающих размер диполя. Для этого в формуле () приведем к общему знаменателю, примем r₁r₂  r², (r₁ – r₂ ) = lcos  и введем .

при r  l

потенциал и напряженность поля диполя на больших расстояниях от него

Формулу для Е (без вывода) приводим только для того, чтобы отметить, что и потенциал, и напряженность поля диполя убывают быстрее ( 1/ r² , E  1/r³), чем в случае одиночного заряда (  1/r, Е 1/r²).

20. Поведение диполя во внешнем однородном электрическом поле. Момент сил, действующих на диполь со стороны поля.

О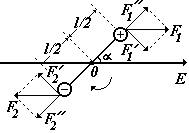 днородное поле. Внесем диполь в однородное внешнее электрическое поле с напряженностью Е. На заряды диполя будут действовать силы F₁ = F₂ = qE . Разложим их на составляющие F₁, F₁ и F₂, F₂ (см.рис.). Составляющие F₁ и F₂ стремятся растянуть диполь, а составляющие F₁ и F₂ создают вращающие моменты и поворачивают диполь (по часовой стрелке) до тех пор, пока он не расположится вдоль силовой линии.

	М1 = М2 – вращающие моменты (моменты сил), векторы моментов направлены от нас  чертежу; результирующий момент равен М = М1 + М2= 2qE(l/2)sin. Учитывая, что рэл = ql, получим:
	вращающий момент (момент сил), действующий на диполь во внешнем поле в скалярной и векторной формах

Таким образом, в однородном внешнем электрическом поле диполь одновременно будет растягиваться и поворачиваться до тех пор, пока не окажется в положении равновесия, при этом его дипольный момент станет параллельным вектору напряженности внешнего поля.

21. Поляризованность диэлектрика(вектор поляризации). Его связь с напряженностью поля в диэлектрике. Электрическая восприимчивость.

Если диэлектрик внести во внешнее электрическое поле, на его поверхностях появляются заряды. Это явление называется поляризацией диэлектриков, а сами заряды называются связанными, так как они могут смещаться только в пределах самой молекулы. При снятии внешнего поля поляризация

практически мгновенно исчезает.

Поляризация диэлектриков характеризуется физической величиной, называемой вектором поляризации (Р):

(Кл/м2)	Здесь: pi – дипольный момент молекулы, V – объем диэлектрика. Вектор поляризации по смыслу представляет собой векторную сумму дипольных моментов всех молекул в единице объема диэлектрика.
	результирующее поле внутри диэлектрика

Электрическое поле в диэлектриках характеризуют также вспомогательным вектором D:

вектор электрической индукции (электрического смещения)

Вектор D физического смысла не имеет, но он удобен в случае, когда линии напряженности внешнего поля перпендикулярны поверхности диэлектрика. В этом случае D в вакууме и в диэлектрике имеет одно и то же значение: D = D_0..⁴

Векторы напряженности E, электрической индукции D и поляризации P связаны между собой соотношением:

Эту формулу можно получить, подставив в () выражения для D и P (предлагаем сделать это самостоятельно).

Податливость вещества явлению электрической поляризации определяется отношением поляризованности к напряженности поля в диэлектрике,это отношение называется электрической восприимчивостью()