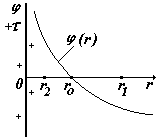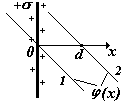- •1.Электрический заряд.Его дискретность.Закон сохранения электрического заряда. Закон кулона в векторном и скалярном виде.
- •5. Циркуляция вектора напряженности электростатического поля. Потенциальный характер электростатического поля.
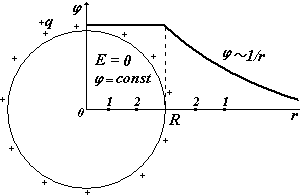
- •11. Получите выражение для потенциала поля равномерно заряженной тонкой сферы. Считайте потенциал равным 0 в бесконечности. Нарисуйте график φ(r) внутри и вне сферы.
- •12. Получите выражение для потенциала бесконечно длинной равномерно заряженной нити. Считайте потенциал равным 0 на расстоянии r0 от нити. Нарисуйте график φ(r).
- •13. Получите выражение для потенциала бесконечно равномерно заряженной плоскости в зависимости от расстояния X от плоскости. Считайте потенциал плоскости равным φ0. Нарисуйте график φ(X).
- •15.Электроемкость уединенного проводника. Выражение для электроемкости сферы.
- •16.Электроемкость конденсатора. Выражение для электроемкости плоского конденсатора.
- •17. Получите выражение для электроемкости при параллельном соединении конденсаторов.
- •19. Диполь и его электрический момент. Напряженность и потенциал поля диполя на его продольной оси. Расстояние от диполя много больше длины диполя.
- •20. Поведение диполя во внешнем однородном электрическом поле. Момент сил, действующих на диполь со стороны поля.
- •21. Поляризованность диэлектрика(вектор поляризации). Его связь с напряженностью поля в диэлектрике. Электрическая восприимчивость.
- •22. Энергия заряженного конденсатора.
- •23.Энергия электростатического поля. Объемная плотность энергии.
- •24.Энергия электростатического поля. Получите выражение для объемной плоскости энергии на примере плоского конденсатора.
- •25. Сила тока. Плотность тока. Выражение для плотности тока через среднюю скорость носителей тока и их концентрацию.
- •26. Постоянный электрический ток. Сторонние силы и эдс источника тока.
- •28. Закон Ома в локальной (дифференциальной) форме. Удельное сопротивление и удельная проводимость.
- •29.Электронная(классическая) теория электропроводности металлов. Основные предположения теории и вывод закона Ома в локальной(дифференциальной) форме.
- •30. Закон Джоуля-Ленца. Формулы для вычисления мощности, выделяющейся на сопротивлении.
- •32. Электрическое сопротивление при параллельном и последовательном соединении проводников.
- •33.Сила Лоренца (в векторной и скалярной формах). Вектор магнитной индукции, его размерность.
- •34. Движение заряженных частиц в магнитном поле. Радиус кривизны и шаг винтовой траектории движения.
- •36. Получите на основе закона Био-Савара выражение для нахождения индукции магнитного поля на оси и в центре кругового витка с током. Магнитный момент витка с током.
- •38. Магнитное поле соленоида. Выражение для индукции магнитного поля внутри бесконечно длинного соленоида.
- •39.Действие магнитного поля на ток. Сила, действующая на элемент тока(закон ампера) в векторной и скалярной формах.
- •40.Действие магнитного поля на ток. Сила, действующая на прямолинейный проводник с током(закон Ампера).
- •41.Сила взаимодействия(на единицу длины) между двумя прямыми параллельными проводниками с токами для одинаково и противоположно направленных токов.
- •42.Вращающий момент, действующий на контур с током в однородном магнитном поле.
- •43.Сила,действующая на контур с током,в неоднородном магнитном поле.
- •44.Поведение витка с током во внешнем однородном магнитном поле. Устойчивое и неустойчивое положение равновесия витка.
11. Получите выражение для потенциала поля равномерно заряженной тонкой сферы. Считайте потенциал равным 0 в бесконечности. Нарисуйте график φ(r) внутри и вне сферы.
Сфера радиуса R, заряженная с поверхностной плотностью заряда (Кл/м2).
Полный заряд на сфере q = 4R2 . Будем рассматривать две области:1) выбираем две любые точки 1 и 2 в этой области и 2) также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
Подставим Е поля сферы. Для получается та же формула, что и для поля точечного заряда. |
|
|
|
|
|
12. Получите выражение для потенциала бесконечно длинной равномерно заряженной нити. Считайте потенциал равным 0 на расстоянии r0 от нити. Нарисуйте график φ(r).
Бесконечно длинная нить, заряженная с линейной плотностью заряда .
Выберем на оси радиальных координат r две любые точки с координатами r1 и r2.
|
В этом случае принять = 0 на бесконечности нельзя (см. график ln x), поэтому выбираем = 0 в некоторой произвольной точке с координатой ro. Т.е. примем
заменим 2 , r2 r получим (r) |
|
= 0 при r = r0 |
|
|
13. Получите выражение для потенциала бесконечно равномерно заряженной плоскости в зависимости от расстояния X от плоскости. Считайте потенциал плоскости равным φ0. Нарисуйте график φ(X).
Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда (Кл/м2). Выберем на оси координат х две произвольные точки х1 и х2 .).
|
Чтобы получить выражение для потенциала примем 1) 1 = 0 при х1 = 0 и 2) 1 = 0 при х1 = d (d – произвольная точка на оси х) |
1) 2) |
|
14. Получите выражение для разности потенциалов между двумя бесконечно протяженными плоскостями,равномерно заряженными разноименными одинаковыми по модулю зарядами(+-)σ.
Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой Е=/0, где — поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно dравна
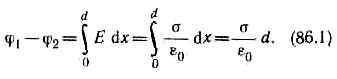
15.Электроемкость уединенного проводника. Выражение для электроемкости сферы.
Все проводники обладают свойством накапливать электрические заряды. Это свойство называется электроемкостью. Количественная характеристика этого свойства также называется электроемкостью и обозначается С. Различают электроемкость уединенного проводника (собственная емкость), находящегося вдали от других проводников, и взаимную емкость системы из двух и более проводников.
(Ф = Кл/В) |
емкость уединенного проводника (собственная емкость)– численно она равна тому заряду, который нужно сообщить проводнику, чтобы изменить его потенциал на единицу |
Фарада – единица измерения емкости в СИ является чрезвычайно большой величиной. Собственная емкость зависит только от формы и размеров проводника и от диэлектрических свойств окружающей среды (вакуум, воздух, керосин,…) и не зависит ни от материала проводника ни от того, заряжен он или нет. Каждый уединенный проводник обладает «своей» емкостью. Вычислим электроемкость уединенной сферы (шара).
|
потенциал заряженной сферы (шара); подставим в (1), получим: |
|
емкость сферы (шара); в вакууме зависит только от радиуса сферы (шара) |



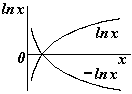 1
= 0 при r1
= r0,
1
= 0 при r1
= r0,