43.Сила,действующая на контур с током,в неоднородном магнитном поле.
В неоднородном магнитном поле кроме сил,присутствующих в однородном магнитном поле, которые поворачивают и растягивают контур, появляется составляющая сил, которая стремится переместить контур. Если контур оказался ориентированным своим магнитным моментом по полю (как на рисунке), то составляющая силы F1 будет растягивать контур, а составляющая F2 будет втягивать контур в область более сильного поля. Если контур окажется в поле таким образом, что его магнитный момент будет направлен против поля, это положение контура будет неустойчивым. Контур развернется по полю, и будет втягиваться в область более сильного поля.
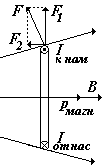Приведем выражение
для силы, действующей на контур с током
в неоднородном магнитном поле, индукция
которого изменяется только по одной
координате х.
|
Сила, действующая на контур (виток) с током в неоднородном магнитном поле В(х). |
44.Поведение витка с током во внешнем однородном магнитном поле. Устойчивое и неустойчивое положение равновесия витка.
Контур
с током, помещенный в магнитное поле,
обладает запасом энергии. Действительно,
чтобы повернуть контур с током на
некоторый угол
в направлении, обратном направлению
его поворота в магнитном поле, необходимо
совершить работу против сил, действующих
на этот контур со стороны поля. По
величине эта работа равна
.
Совершенная над контуром работа идет на увеличение его энергии. Поворачиваясь в первоначальное положение, контур возвратит затраченную на его поворот работу, совершив ее над какими-либо телами. Следовательно, запасенная контуром энергия есть:
.
(при
выводе этой формулы мы приняли, что при
энергия контура W,
определенная с точностью до произвольной
постоянной, равна нулю).
Полученную формулу можно написать также в виде:
Устойчивое равновесие |
Неустойчивое равновесие |
Рис.9.3. Положения равновесия контура с током в магнитном поле.
Из
приведенной формулы видно, что устойчивому
положению равновесия контура с током
в магнитном поле (рис.9.3) соответствует
ориентация, при которой векторы
и
параллельны (α
= 0); в этом случае
энергия контура минимальна
и равна
.
Неустойчивому
положению равновесия соответствует
ориентация, при которой векторы
и
антипараллельны (α
= π); в этом
случае энергия контура максимальна
и равна
.
1
2
3 Не обязательно брать цилиндр, можно взять любую призму, важно, чтобы ее образующие были перпендикулярны торцевым сечениям и самой заряженной плоскости.
4
5
6
7