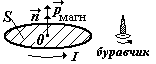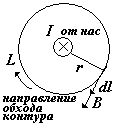34. Движение заряженных частиц в магнитном поле. Радиус кривизны и шаг винтовой траектории движения.
35. Выражение для магнитной индукции поля элемента тока(закон Био-Савара) в векторной и скалярной формах. Сделайте соответствующий чертеж. Принцип суперпозиции для магнитного поля.
|
при дискретном распределении проводников с током |
Принцип суперпозиции для магнитных полей: «Если магнитное поле создается несколькими токами, то магнитная индукция результирующего поля равна векторной сумме индукций полей отдельных токов» |
|
при непрерывном распределении тока в проводнике |
Смысл принципа суперпозиции в том, что, как и в случае электростатических полей, магнитные поля складываются независимо, т.е. не влияя друг на друга.
|
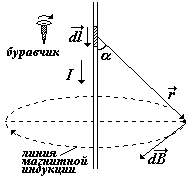
Закон Био-Савара-Лапласа в векторной и скалярной формах; dB – магнитная индукция, создаваемая бесконечно малым элементом проводника dl, по которому течет ток I, в точке с радиус-вектором r. |
|
Пользуясь законом БСЛ и принципом суперпозиции можно найти выражения для индукции магнитных полей различных проводников с током.
36. Получите на основе закона Био-Савара выражение для нахождения индукции магнитного поля на оси и в центре кругового витка с током. Магнитный момент витка с током.
Магнитное поле на оси кругового тока.
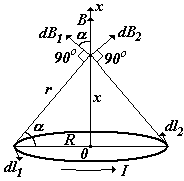
На рисунке показаны линии магнитной индукции поля кругового тока (половина поля). Это сложное трехмерное поле, аналитической формулы для которого не существует. Мы получим выражение для магнитной индукции только на оси кольца.
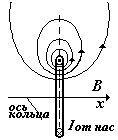Выделим на кольце
с током два элемента dl1
и dl2
, расположенных диаметрально противоположно
(см. рис. ниже). Магнитные индукции от
этих элементов dB1
и dB2
. Если разложить эти векторы на составляющие
вдоль оси х
и в перпендикулярном к ней направлении,
то перпендикулярные составляющие
взаимно компенсируются, а составляющие
по оси х будут
складываться. К этому же мы придем,
рассматривая подобные элементы по всему
кольцу. Таким образом, магнитная индукция
на оси кольца направлена вдоль оси
кольца (по правилу буравчика).
|
магнитная индукция от элементов dl1 и dl2 |
|
|
составляющая магнитной индукции по оси х |
|
|
угол для данной точки на расстоянии х по оси кольца постоянная величина |
|
|
||
Магнитное поле в центре кругового тока
Это частный случай предыдущего примера, когда х = 0
|
Магнитная индукция в центре кругового тока |
|
Контур с током (виток с током) при изучении магнитных свойств вещества имеет такое же значение, как диполь при изучении электрических свойств вещества. Рассматривая поведение витка с током во внешнем магнитном поле, можно качественно объяснить намагниченность различных веществ. Контур с током характеризуют векторной величиной рмагн магнитным моментом.
|
магнитный момент контура с током I - сила тока в контуре, S – площадь, охватываемая контуром, n- нормаль к площади контура |
|
37.Теорема о циркуляции вектора магнитной индукции. Получите с помощью этой теоремы выражение для нахождения индукции магнитного поля бесконечно длинного проводника с током.
|
=
|
Теорема о циркуляции вектора магнитной индукции: «Циркуляция вектора индукции магнитного поля по любому замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром, умноженной на o». |
=
|
()
()Выражение () применяется в случаях дискретного распределения проводников с токами, т.е. когда имеются отдельные проводники с токами и требуется найти индукцию В поля вне проводников. Выражение () используется в случаях, когда требуется найти индукцию В магнитного поля внутри проводника с током, т.е. при непрерывном распределении тока по проводнику.
Прямой бесконечный проводник с током.
При использовании теоремы о циркуляции, нужно выбрать такую замкнутую кривую (контур L), в каждой точке которой индукция В была бы одинаковой по величине. Тогда В можно будет вынести из-под интеграла. В случае прямого тока линии индукции – концентрические окружности, и выбрав одну из линий индукции в качестве контура L, получим Вl = Вcos = B(cos = 1) (см.рис.). Запишем ().
|
теорема о циркуляции вектора магнитной индукции |
|
|
вынесем В= const, интеграл даст 2 r; т.о. найдем индукцию магнитного поля длинного прямого тока более простым способом, чем по закону БСЛ |
