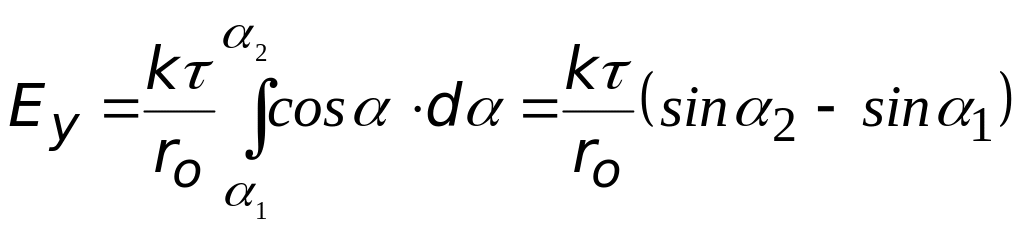1.Электрический заряд.Его дискретность.Закон сохранения электрического заряда. Закон кулона в векторном и скалярном виде.

Электрический заряд-физическая величина, определяющая способность тел к электромагнитным взаимодействиям

Опытным путем (1910—1914) амери­канский физик Р. Милликен (1868 — 1953) показал, что электрический заряд дискре­тен, т. е. заряд любого тела составляет целое кратное от элементарного электриче­ского заряда е (e= 1,6•10^-19 Кл). Элек­трон (т_е = 9,11•10^-31 кг) и протон (т_р=1,67•10^-27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов

Из обобщения опытных данных был установлен фундаментальный закон при­роды, экспериментально подтвержденный в 1843 г. английским физиком М. Фараде­ем (1791 —1867),— закон сохранения за­ряда: алгебраическая сумма электриче­ских зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы.

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, про­порциональна зарядам Q₁ и Q₂ и обратно пропорциональна квадрату расстояния r между ними:

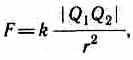
где k — коэффициент пропорционально­сти, зависящий от выбора системы единиц.

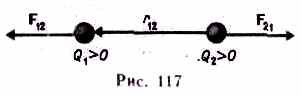
Сила F направлена по прямой, соеди­няющей взаимодействующие заряды, т. е. является центральной, и соответству­ет притяжению (F<0) в случае разно­именных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эта сила называется кулоновской силой.

В векторной форме закон Кулона име­ет вид

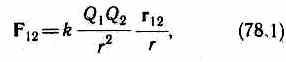
где F₁₂— сила, действующая на заряд Q₁ со стороны заряда Q₂, r₁₂ — радиус-век­тор, соединяющий заряд Q₂ с зарядом Q₁, r= |r₁₂| (рис. 117). На заряд Q₂ со сторо­ны заряда Q₁ действует сила F₂₁=-F₁₂, т. е. взаимодействие электрических точеч­ных зарядов удовлетворяет третьему за­кону Ньютона.

В СИ коэффициент пропорционально­сти равен

k=1/(4₀).

Тогда закон Кулона запишется в оконча­тельном виде:

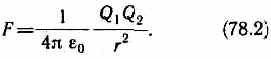
2.Напряженность электростатического поля. Выражение для напряженности электростатического поля точечного заряда в векторном и скалярном виде. Электрическое поле в вакууме и в веществе. Диэлектрическая проницаемость.

Для обнаружения и опытного исследо­вания электростатического поля использу­ется пробный точечный положительный заряд — такой заряд, который не искажа­ет исследуемое поле (не вызывает пере­распределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, по­местить пробный заряд Q₀, то на него действует сила F, различная в разных точках поля, которая, согласно закону Ку­лона (78.2), пропорциональна пробному заряду Q₀. Поэтому отношение F/Q₀ не зависит от Q₀ и характеризует электриче­ское поле в той точке, где пробный заряд находится. Эта величина называется на­пряженностью и является силовой харак­теристикой электростатического поля.

Напряженность электростатического поля в данной точке есть физическая вели­чина, определяемая силой, действующей на единичный положительный заряд, по­мещенный в эту точку поля:

E=F/Q₀. (79.1)

Как следует из формул (79.1) и (78.1), напряженность поля точечного заряда

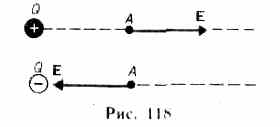
в вакууме

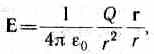
или в скалярной форме

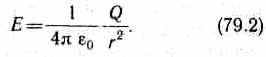
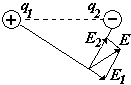
Направление вектора Е совпадает с на­правлением силы, действующей на поло­жительный заряд. Если поле создается положительным зарядом, то вектор Е на­правлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 118).

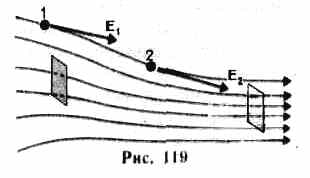
Графически электростатическое поле изображают с помощью линий напряжен­ности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 119). Линиям напряжен­ности приписывается направление, со­впадающее с направлением вектора на­пряженности. Для однородного поля (когда вектор на­пряженности в любой точке постоянен по

131

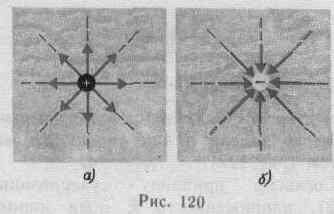
величине и направлению) линии напря­женности параллельны вектору напряжен­ности. Если поле создается точечным за­рядом, то линии напряженности — ради­альные прямые, выходящие из заряда, если он положителен (рис. 120, а), и вхо­дящие в него, если заряд отрицателен (рис. 120, б).

Величина ₀ называется электрической постоянной; она относится к числу фунда­ментальных физических постоянных и равна

₀=8,85•10^-12Кл²/(Н•м²),

или

₀=8,85•10^-12Ф/м, (78.3)

где фарад (Ф) — единица электрической емкости (см. §93). Тогда

1/(4₀) = 9•10⁹м/Ф.

3.Потенциал электростатического поля. Общее выражение, связывающее потенциал с напряженностью. Получите выражение для потенциала поля точесного заряда, исходя из выражения для напряженности этого поля.

(В = Дж/Кл)

потенциал (скаляр) – энергетическая характеристика электростатического 1 поля  по смыслу это: 1) потенциальная энергия, которой обладает единичный положительный заряд, помещенный в данную точку поля или 2) работа, которую надо совершить, чтобы перенести единичный положительный заряд из данной точки 1 в бесконечность ().

разность потенциалов – это работа, которую надо совершить, чтобы переместить единичный положительный заряд из точки 1 в точку 2

Найдем связь между напряженностью и потенциалом.

	работа в потенциальном (консервативном) поле равна убыли потенциальной энергии
dx ,  перемещение	выразим элементарную работу через напряженность и разность потенциалов; сократим на q, обозначим проекцию вектора Е на направление х как Ех, получим:
()		связь между Е и  в дифференциальной форме для одномерного случая, когда потенциал зависит только от координаты х   (х)

	В трехмерном случае, когда потенциал является функцией  (х,y,z), запишем формулы для каждой проекции и, объединяя их в одно выражение, найдем (учитывая, что Е  вектор):
	 («набла»)  другое обозначение градиента (модуль вектора Е)	Напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком.

Градиент – это вектор, показывающий направление наибольшего роста скалярной функции (в нашем случае - потенциала).² В одномерном случае градиент напряженности d / dx приобретает простой физический смысл: он показывает, на сколько изменяется потенциал на единице длины.

«» в правой части формул означает, что вектор напряженности Е всегда направлен в сторону убывания потенциала.

Из приведенных выражений, зная  (х,y,z), можно, дифференцируя, найти напряженность поля. Производя обратную операцию – интегрирование, можно при известной напряженности найти потенциал. Рассмотрим случай зависимости

Е и  только от одной переменной х. Из формулы () находим:

()

Связь разности потенциалов с напряженностью в интегральной форме для одномерного случая, когда Е(х)

4.Принцип суперпозиции как фундаментальное свойство полей. Общее выражение для напряженности и потенциала поля, создаваемого в точке с радиусом вектором r системой точечных зарядов qi, находящихся в точках с координатами ri.

На основе опытных данных был получен принципа суперпозиции (наложения) полей: «Если электрическое поле создается несколькими зарядами, то напряженность и потенциал результирующего поля складываются независимо, т.е. не влияя друг на друга». При дискретном распределении зарядов напряженность результирующего поля равна векторной сумме, а потенциал алгебраической (с учетом знака) сумме полей, создаваемых каждым зарядом в отдельности. При непрерывном распределении заряда в теле векторные суммы заменяется на интегралы, где dE и d– напряженность и потенциал поля элементарного (точечного) заряда, выделенного в теле. Математически принцип суперпозиции можно записать так.

		при дискретном распределении зарядов	принцип суперпозиции
		при непрерывном распределении зарядов

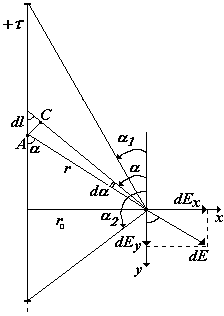
В качестве примера получения выражения для напряженности поля с помощью принципа суперпозиции найдем напряженность поля тонкого стержня конечной длины, равномерно заряженного с линейной плотностью заряда 

Выберем бесконечно малый элемент dl стержня с зарядом dq. Поскольку напряженности от различных элементов направлены по-разному, введем оси проекций х и у. Итегрируя, найдем результирующие напряженности Е_х и Е_у.

	dE- напряженность от элемента стержня dl с зарядом dq = dl, dEх и dEy – проекции dE на направления х и у.
	Чтобы проинтегрировать, сведем к одной переменной 
	длина дуги АС при малых углах, она же из треугольника (А, С, dl)
				модуль напряженности

Для бесконечно длинной нити 1  0, 2  180о, следовательно, Еу = 0 и Е = Ех (cos180o = 1), r – расстояние от точки, в которой определяется напряженность, до нити.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов: 

φ = φ1 + φ2 + φ3 + ..