24.Способы расчета среднего темпа роста для монотонного ряда динамики.

Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.

Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:

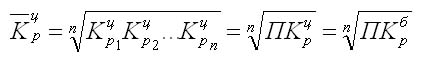
где n — число цепных коэффициентов роста; Кц — цепные коэффициенты роста; Кб — базисный коэффициент роста за весь период.

Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.

Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:

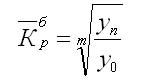
25.Средние арифметические взвешенные, их построение и свойства.

Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.

Представим это в виде следующей формулы:

— цена за единицу продукции;

— количество (объем) продукции;

Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.

2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:

3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:

4.Сумма квадратов отклонений вариантов от средней меньше, чем сумма квадратов отклонений от любой другой произвольной величины , т.е:

5. Если все варианты ряда уменьшить или увеличить на одно и то же число , то средняя уменьшится на это же число :

6.Если все варианты ряда уменьшить или увеличить в раз, то средняя также уменьшится или увеличится в раз:

7.Если все частоты (веса) увеличить или уменьшить в раз, то средняя арифметическая не изменится:

26.Общая характеристика показателей вариации и их назначение.

Показатели вариации – дают характеристику однородности изучаемой совокупности, являются инструментом для изучения взаимосвязей между результативными и факторными показателями.

1)Размах вариации R=Xmax-Xminэто разность между максимальным и минимальным значениями признака

2)Среднее линейное отклонение это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

3)Среднее квадратическое отклонение используется для практической оценки величины вариации расчетом +/-Кσ, К=1,2,…,nравно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической

4)Дисперсия – наиболее общая мера вариации признака. На основании дисперсии можно увидеть количество, меру влияния всех причин на вариацию признака. Можно видеть те причины, которые в наибольшей мере вызывают вариацию признака.

Если данные сгруппированы,

5)Коэффициент вариации *100% является приближенной мерой однородности.