17. Математическое ожидание случайной величины и его свойства.

Определение. Математическим ожиданием  непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

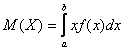
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

 При этом, конечно, предполагается, что несобственный интеграл сходится.

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:

М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п . (7.1)

Если число возможных значений случайной величины бесконечно, то , если полученный ряд сходится абсолютно.

Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.

Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.

Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.

Свойства математического ожидания.

1. Математическое ожидание постоянной равно самой постоянной:

М(С) = С. (7.2)

Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С.

2. Постоянный множитель можно выносит за знак математического ожидания:

М(СХ) = С М(Х). (7.3)

Доказательство. Если случайная величина Х задана рядом распределения

xi	x1	x2	…	xn
pi	p1	p2	…	pn

то ряд распределения для СХ имеет вид:

Сxi	Сx1	Сx2	…	Сxn
pi	p1	p2	…	pn

Тогда М(СХ) = Сх₁р₁ + Сх₂р₂ + … + Сх_пр_п = С( х₁р₁ + х₂р₂ + … + х_пр_п) = СМ(Х).

Математическим ожиданием непрерывной случайной величины называется

(7.13)

Замечание 1. Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной (опр. 7.5), а формула для ее вычисления имеет вид:

(7.14)

Среднее квадратическое отклонение вычисляется по формуле (7.12).

Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a, b], то интегралы в формулах (7.13) и (7.14) вычисляются в этих пределах.