О применимости предельных теорем в схеме Бернулли

Следует различать ситуации, когда к схеме Бернулли можно применить пуассоновскую, а когда нормальную аппроксимации. Из формулировок теорем Пуассона и Муавра-Лапласа, а также Замечания 4 можно вывести следующие общие правила:

1.Если   велико, а   не велико, следует пользоваться пуассоновским приближением;

2.Если   велико и   велико, то можно применять нормальное приближение.

На практике в ситуации, когда   имеет порядок сотен, поступают следующим образом: если  , то применяют пуассоновское приближение; если же   имеет порядок нескольких десятков, топользуются нормальной аппроксимацией.

12. Локальная и интегральная теорема Муавра-Лапласа.

Локальная теорема Лапласа

Использование формулы Бернулли при больших значениях   требует выполнения арифметических действий над огромными числами, что обусловлено наличием факториалов в формуле для числа сочетаний. Поэтому, если число испытаний   достаточно велико, то для нахождения вероятности появления события   ровно   раз применяют следующую теорему. Теорема. Если вероятность   появления события   в каждом испытании постоянна и отлична от нуля и единицы, то вероятность   того, что событие   появится в   испытаниях ровно   раз, приближенно равна (тем точнее, чем больше  ) значению функции . 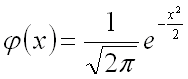Для положительных значений аргумента значения функции   приведены в специальной таблице. Для отрицательных значений аргумента пользуются той же таблицей и свойством четности функции  , то есть  . Таким образом, вероятность того, что событие   появится в   испытаниях ровно   раз, приближенно равна , где  .

Интегральная теорема Лапласа

Теорема. Если вероятность   появления события   в каждом испытании постоянна и отлична от нуля и единицы, то вероятность   того, что событие   появится в   испытаниях от   до   раз, приближенно равна определенному интегралу , где  . При решении задач, требующих применения интегральной теоремы Лапласа, используют специальную таблицу для интеграла  . В ней приведены значения функции  (которую называют функцией Лапласа) для  . Если  , то принимают  . Для  пользуются той же таблицей и свойством нечетности функции Лапласа, то есть  . Для того чтобы можно было пользоваться таблицей, преобразуем формулу из интегральной теоремы Лапласа: Таким образом, вероятность того, что событие   появится в   испытаниях от   до   раз, может быть вычислена по формуле   , где  .

13. Дискретные случайные события и возможности их описания.

Рассмотрим случайную величину *  , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина  примет значение xi

(16)

   Такая случайная величина  называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательностиx1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина  принимает всегда какое-либо значение из области ее изменения, то

Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика.

Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

Заметим, что событие, заключающееся в том, что случайная величина примет одно из своих возможных значений, является достоверным, поэтому

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x_i, p_i).

x₁ x₂ x₃ x₄ x₅

14. Закон распределения дискретной случайно величины. Многоугольник распределения.

  Определение.  Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

            Закон распределения может быть задан аналитически, в виде таблицы или графически.

            Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x₁,x₂,...x_n) и соответствующими им вероятностями (p₁,p₂,... ,p_n). При этом события (x₁,x₂,...x_n) образуют полную группу (т.е. появление одного из них является достоверным событием), что означает

                                                                                     (1)

Про случайную величину X в таком случае говорят, что она подчинена данному закону распределения.

Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Возможное значение X	X1	Х2	...	Хn
Вероятность	Р1	Р2	...	Рn

Такая таблица называется таблицей распределения (вероятностей) случайной величины X.

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x_i, p_i).

x₁ x₂ x₃ x₄ x₅

            Графическое представление этой таблицы называется многоугольником распределения.  При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.