30. Бесконечно малые и бесконечно большие функции, теорема об их связи. Теорема о связи функции со своим пределом. Некоторые свойства бесконечно малых и бесконечно больших функций.

Если при предел функции , то она называется ббф при .

f(x) – ббф при

Если при предел функции , то она называется бмф при .

f(x) – бмф при .

Теорема о связи ббф и бмф) Если функция – бмф при и , то функция является ббф при . Верно и обратное. Доказательство: Аналогично соответствующему свойству для бм и бб последовательностей.

Теорема о связи функции, её предела и бм) Предел f(x) при равен А тттк бм при функция такая, что

, что . Доказательство: дословно повторяет аналогичное доказательство для последовательности.

31. Первый замечательный предел

Доказательство:

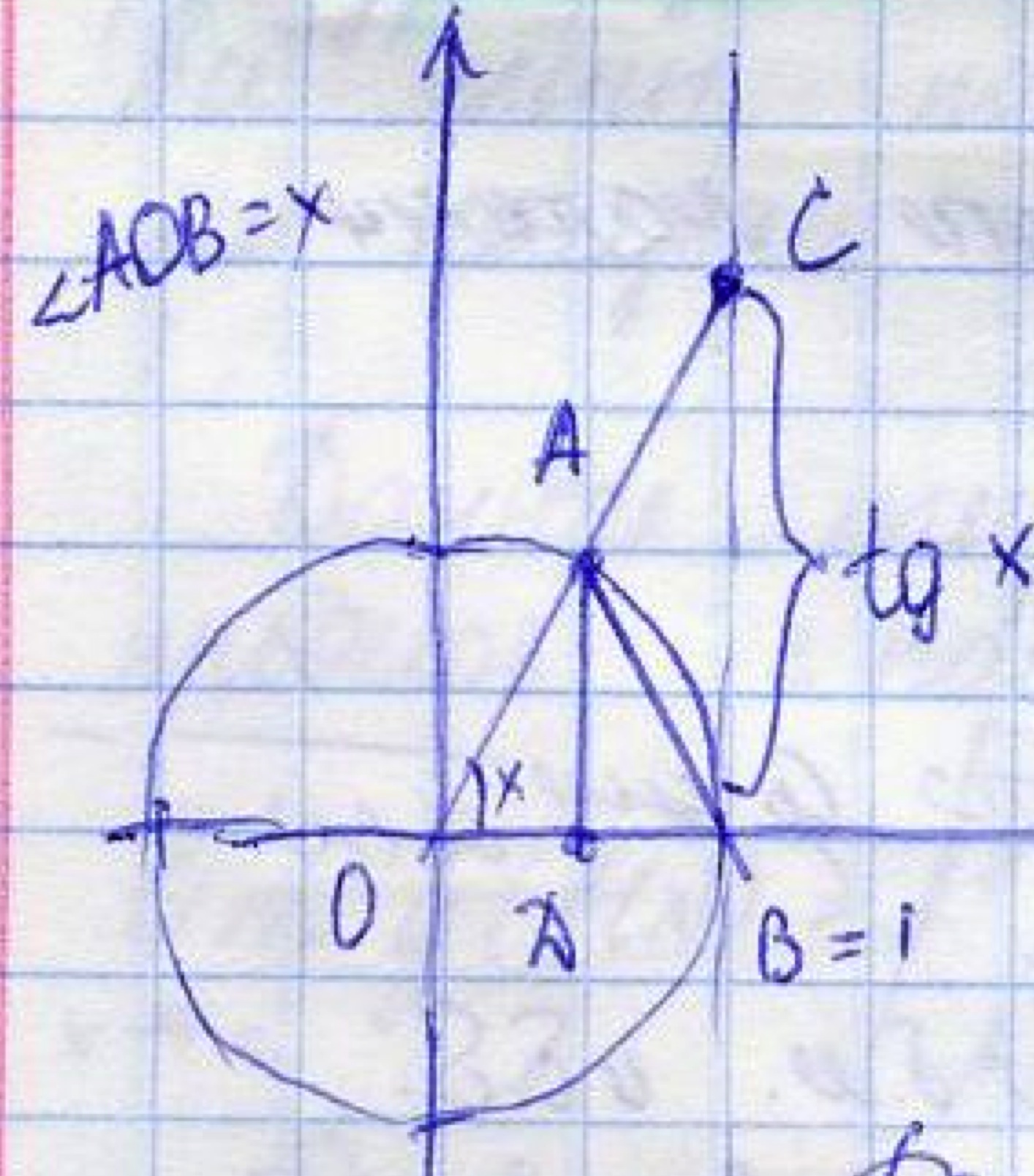
Рассмотрим окружность единичного радиуса с центром в начале координат. Обозначим . Пусть , тогда длина BA=x (дуги), пусть , и – площади , сектора AOB и .

; ;

Поскольку фигура AOB лежит в секторе ACB, а сектор лежит в , то . ;

Поскольку в I четверти sin x>0, то ; . По теореме о зажатой функции ; ; . Поскольку функция является чётной, то когда все последние выкладки также будут истинными.

32. Сравнение бесконечно малых функций. Символы “о-малое” и “О-большое” Пусть (х) и (х) - две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно малыми в точке а. .

1. Говорят, что (х) является в точке а бесконечно малой более высокого порядка, чем (х), если и пишут (читается: « равно о малому от »).
 Итак, символ обозначает любую бесконечно малую в данной точке а функцию, имеющую в этой точке более высокий порядок малости, чем бесконечно малая в той же точке функция (х).

2. Говорят, что (х) и (х) являются в точке а бесконечно малыми оного порядка малости, если предел .

3. Говорят, что а (х) и (х) являются в точке а эквивалентными бесконечно малыми, если предел равен единице.

Теорема1) Следующие условия являются эквивалентными:

1. f(x)=o(g(x)) при ;

2. ;

3. f(x)= *g(x), где ;

Доказательство: Эквивалентность 1,2 следует из определения. Докажем эквивалентность 2,3: ) Т.к. по свойству связи между функцией, её пределом и бм, найдётся такая, что =0+ , ; ) Поделив равенство на g(x), получаем, перейдя к пределу

Определение) Говорят, что бм при имеет k-й порядок малости по сравнению с бм , если

*Для определения ббф существуют аналогичные бмф понятия, но при этом слова «одного порядка малости» заменяют на «одного порядка роста»

33. Эквивалентные функции. Определение. Свойства. Критерий эквивалентности функций. Главная часть функции

Пусть f(x) и g(x) определены в некоторой окрестности (возможно проколотой) точки а и g(x) в этой проколотой окрестности. Опр) Функции f(x) и g(x) называется эквивалентными (асимптотически равными) при , если . В этом случае пишут f(x) g(x) при .

Теор2) Для того чтобы f(x) и g(x) были эквивалентны при необходимо и достаточно, чтобы f(x)=g(x)+o(g(x)) при . Доказательство: ) Пусть f(x) и g(x) эквивалентны. Тогда выполняется и согласно теореме о связи функции, её предела и бм , где при ,

f(x)=g(x)+ (4)

) Пусть выполняется (4). Тогда и переходя к получаем формулу , что и доказывает данная теорема.

Сл1) Если , то

Сл2) Разность эквивалентных бм есть бы более высокого порядка малости, чем каждая из них. Опр) Если f(x)=g(x)+o(g(x)) при , то g(x) называется главной частью функции f(x) при .