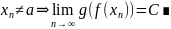- •Способы задания множеств. Отношения между множествами. Операции над множествами.
- •Символы математической логики.
- •Необходимое и достаточное условия. Доказательство методом «от противного». Правило построения отрицания.
- •Типы отображений. Обратимость отображения.
- •Числовые множества. Окрестности и их свойства.
- •Дать определения: а)числовой последовательности; б) ограниченной числовой последовательности; в) предела числовой последовательности. Дать геометрическую интерпретацию этих определений.
- •Сформулировать и доказать свойства сходящейся последовательности (единственность предела, ограниченность)
- •Сформулировать и доказать свойства последовательностей, связанные с неравенствами
- •10. Сформулировать и доказать теорему о пределе «зажатой» последовательности
- •Бесконечно большие и бесконечно малые последовательности.
- •Признак сходимости монотонной последовательности
- •18. Подпоследовательности. Теорема Больцано-Вейерштрасса.
- •22. Конечный предел функции при . Геометрическая иллюстрация. Горизонтальные асимптоты.
- •24. Свойства функций, имеющих конечный предел (единственность, ограниченность, сохранение знака функцией)
- •30. Бесконечно малые и бесконечно большие функции, теорема об их связи. Теорема о связи функции со своим пределом. Некоторые свойства бесконечно малых и бесконечно больших функций.
- •31. Первый замечательный предел
- •33. Эквивалентные функции. Определение. Свойства. Критерий эквивалентности функций. Главная часть функции
- •34. Применение эквивалентных функций к вычислению пределов. Теоремы 3 и 4
- •35. Асимптоты графика функции.
- •38. Два определения функции, непрерывной в точке. Доказательство их эквивалентности.
- •39. Точки разрыва функции и их классификация
- •44.Теорема об ограниченности непрерывной на отрезке функции
- •46. Теорема о непрерывности обратной функции
- •47. Определение и геометрическая интерпретация равномерной непрерывности. Теорема Кантора.
- •48. Определение производной функции в точке. Односторонние производные. Примеры функций, не имеющих производных в точке.
- •49. Механический и геометрический смысл производной. Уравнение касательной и нормали к кривой.
- •50. Определение функции, дифференцируемой в точке. Теоремы о связи дифференцируемости и производной, дифференцируемости и непрерывности.
- •51. Вывод формул производных суммы, произведения и частного функций
- •52. Теорема о производной сложной функции.
- •53. Теорема о производной обратной функции.
- •54. Дифференцированные функции, заданных параметрически и неявно.
- •55. Определение дифференциала, его геометрический смысл. Теория об эквивалентности дифференциала и приращения функции и ее применение к приближенным вычислениям.
- •56. Определение производных и дифференциалов высших порядков. Примеры. Производные высших порядков от функций, заданных параметрически, от неявных функций.
- •58. Теорема Ферма
- •59. Теорема Ролля и её геометрический смысл
- •60. Теорема Лагранжа о конечных приращениях и геометрический смысл.
- •61. Теорема Коши.
- •62. Правило Лопиталя раскрытия неопределенностей 0/0 и ∞/∞
- •63. Формула Тейлора с остатком в форме Пеано
- •64. Единственность формулы Тейлора
- •65. Формула Тейлора с остатком в форме Лагранжа
- •66. Теорема о необходимых и достаточных условиях возрастания и убывания дифференцируемой функции.
- •67. Необходимое условие существования экстремума.
- •68. Первое достаточное условие существования экстремума.
- •69. Второе достаточное условие существования экстремума.
- •70. Наибольшее и наименьшее значения функции на данном отрезке.
- •71. Определение выпуклой и вогнутой функции. Достаточный признак выпуклости и вогнутости.
- •72. Определение точки перегиба. Необходимое условие существования точки перегиба.
- •73. 1 И 2 достаточные признаки точки перегиба.
22. Конечный предел функции при . Геометрическая иллюстрация. Горизонтальные асимптоты.
Понятие
предела функции при очень похоже на
понятие предела последовательности и
имеют с ним много общих черт. Запишем
эти определения в символьной форме и
дадим им геометрическую интерпретацию.
 ;
;
 ;
;
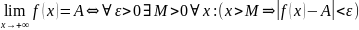
Поскольку
условие
 ,
что означает, что значения функции лежат
в 1-й полосе точки А, то с геометрической
точки зрения это означает, что, начиная
с некоторого числа M
(по смыслу
достаточно большого), значения функции
отличаются от Ф меньше, чем на
.
,
что означает, что значения функции лежат
в 1-й полосе точки А, то с геометрической
точки зрения это означает, что, начиная
с некоторого числа M
(по смыслу
достаточно большого), значения функции
отличаются от Ф меньше, чем на
.
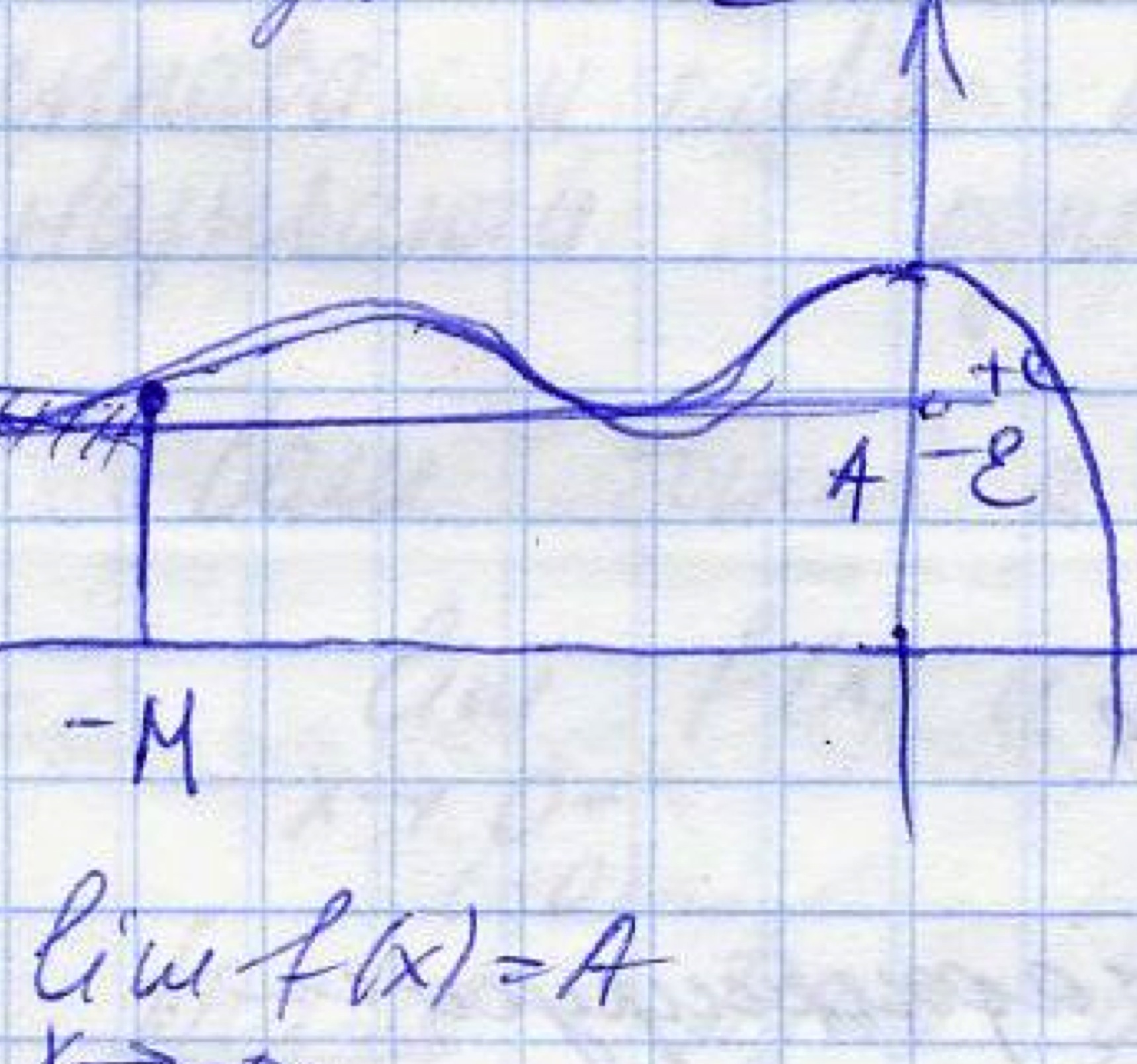
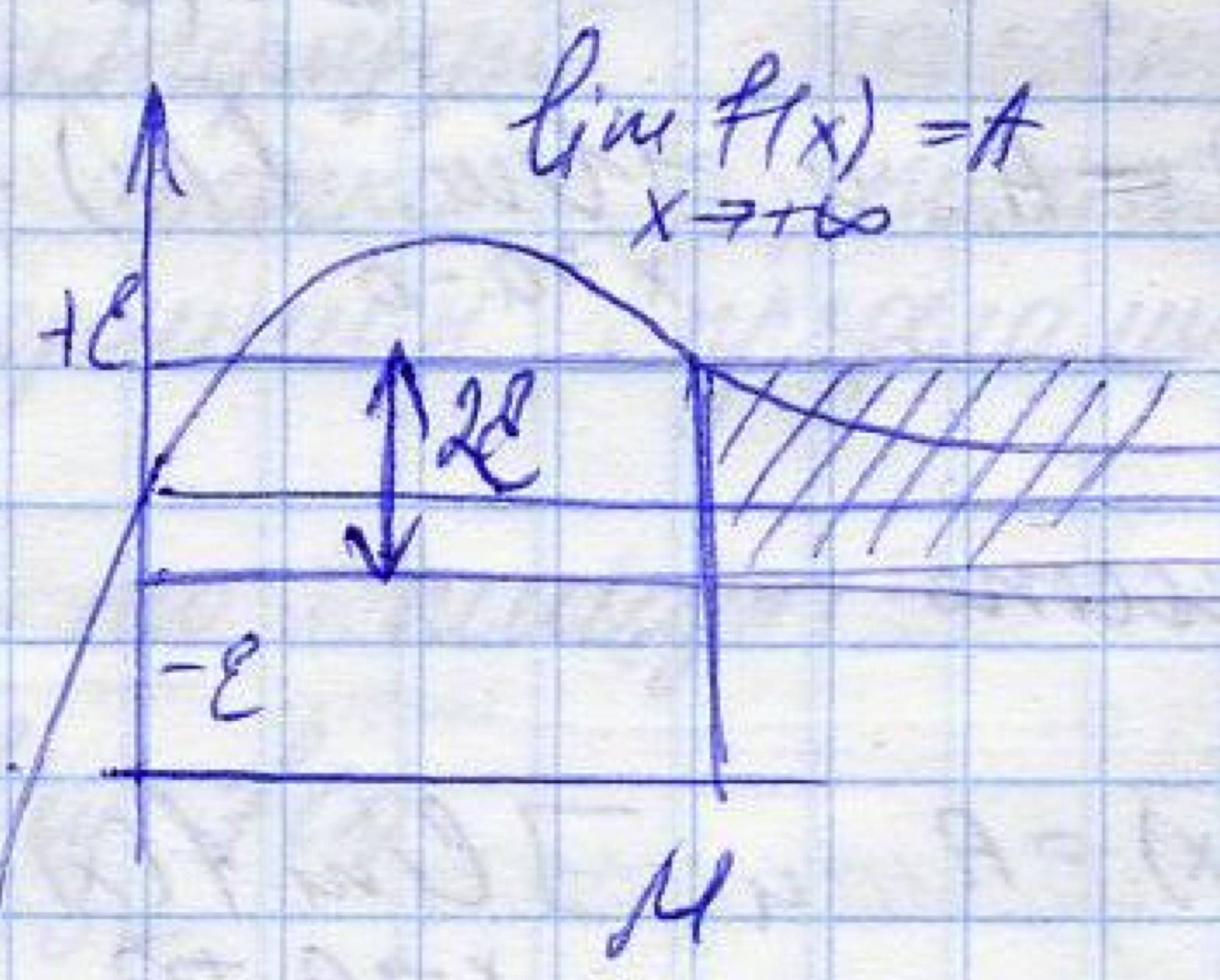
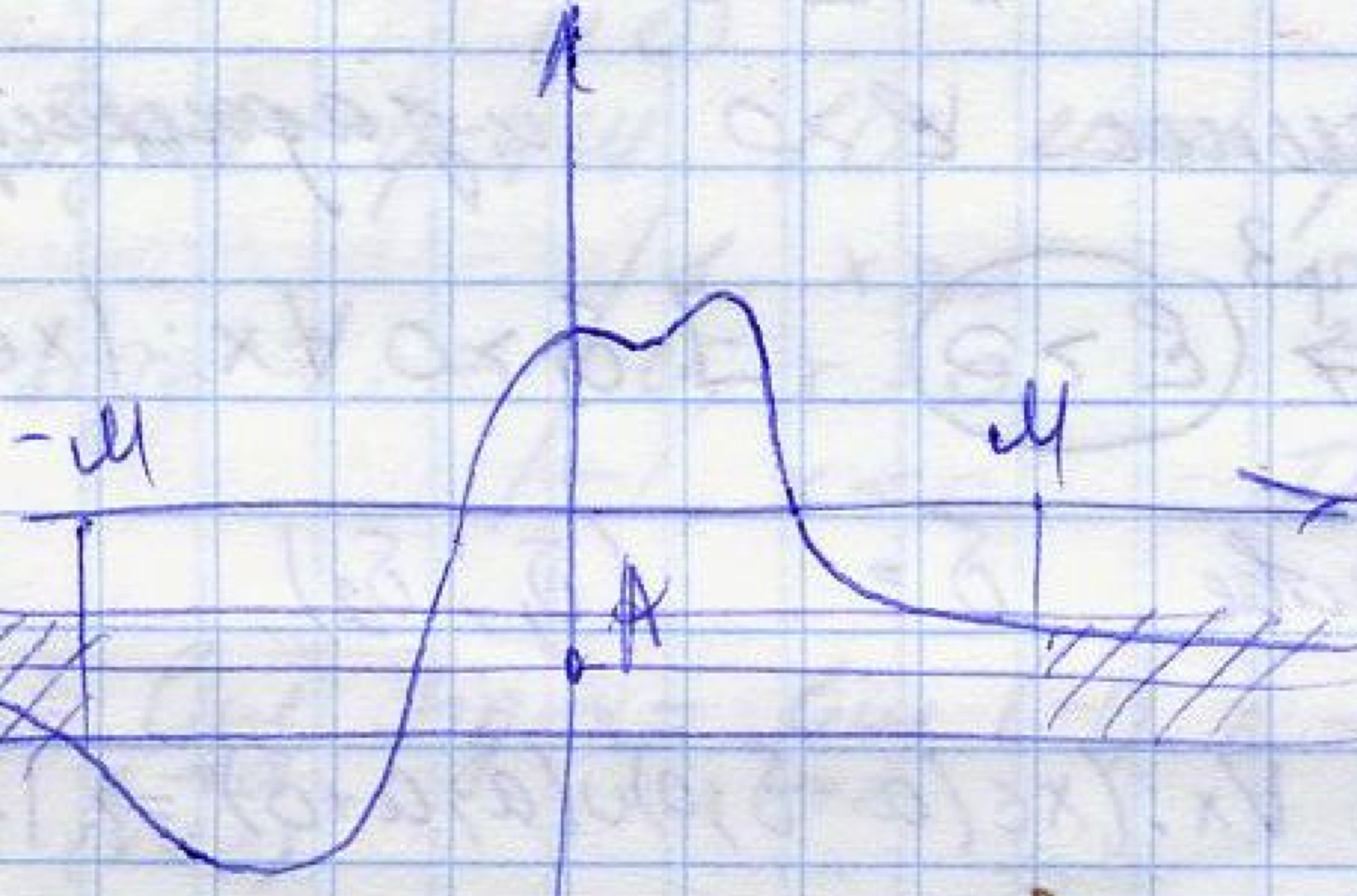
Мы видим, что при больших значениях х, график функции f(x) неограниченно приближается к прямой у=А. Такую прямую принято называть горизонтальной асимптотой. Замечание) Вообще говоря, на (- ) (+ ) функции f(x) может иметь разные горизонтальные асимптоты.
23. Бесконечный предел функции в конечной точке. Геометрическая иллюстрация. Вертикальные асимптоты.
Пусть
функция f(x)
определена
в некоторой окрестности точки а, кроме,
может быть, самой точки а. Орп) Говорят,
что функция f(x)
имеет
в точке
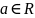 бесконечный предел и пишут
бесконечный предел и пишут
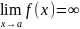 ,
если
,
если
 .
Такие
функции называются бесконечно большими
или стремящимися к
.
Если для некоторых значений аргументы,
приближенные к точки а, функция f(x)
принимает
только отрицательные или только
положительные значения, то пишут
.
Такие
функции называются бесконечно большими
или стремящимися к
.
Если для некоторых значений аргументы,
приближенные к точки а, функция f(x)
принимает
только отрицательные или только
положительные значения, то пишут
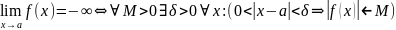 ;
;
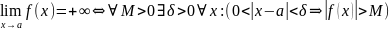 .
Геометрически определение ббф означает,
что для любого M>0
(по
смыслу достаточно большого) мы можем
подойти к предельной точке а настолько
близко, что значение функции в этих
точках превзойдут выбранное M.
.
Геометрически определение ббф означает,
что для любого M>0
(по
смыслу достаточно большого) мы можем
подойти к предельной точке а настолько
близко, что значение функции в этих
точках превзойдут выбранное M.
Существование у функции f(x) бесконечного предела в конечной точке а означает, что график функции неограниченно приближается к прямой х=а, а значит эта прямая является вертикальной асимптотой данной функции.
24. Свойства функций, имеющих конечный предел (единственность, ограниченность, сохранение знака функцией)
Свойство1)
(единственность пределов) Если функция
f(x)
в
точке а имеет предел, то он единственный.
Доказательство: Предположим противное,
что функция f(x)
имеет 2 предела:
 и
и
 ,
но тогда для любой последовательности
{
}:
,
согласно
определению предела функции по Гейне
последовательность значений {f(
,
но тогда для любой последовательности
{
}:
,
согласно
определению предела функции по Гейне
последовательность значений {f(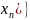 должна
стремиться к
и к
(
должна
стремиться к
и к
( ),
что противоречит единственности предела
сходящейся последовательности.
),
что противоречит единственности предела
сходящейся последовательности.
Свойство2)
(локальная ограниченность) Если функция
f(x)
имеет
предел в точке а, то найдётся такая
окрестность в точке а, в которой функция
ограничена. Доказательство: Пусть
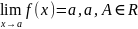 ,
тогда
для
,
тогда
для
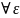 ,
а значит и для
,
а значит и для
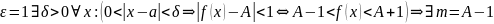 и
и

Свойство3) (сохранение знака) Если функция f(x) имеет конечный предел в точке а, отличный от 0, то найдётся такая окрестность точки а, в которой функция f(x) имеет знак своего предела.
25. Теорема о пределе зажатой функции
Если
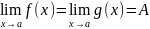 и существует такая окрестность в точке
а (возможно проколотая), что
и существует такая окрестность в точке
а (возможно проколотая), что
 ,
то
,
то
 .
Доказательство: Пусть
.
Доказательство: Пусть
 (*). Т.к.
(*). Т.к.
 для некоторого
для некоторого
 (**) Аналогично для
(**) Аналогично для
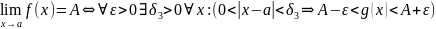 (***) В результате мы получаем
(***) В результате мы получаем
 ;
;
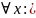

26. Предел суммы функций
 .
Возьмём произвольное
и зафиксируем его.
.
Возьмём произвольное
и зафиксируем его.


Выбираем
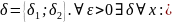
27. Предел произведения функций
 .
Возьмём
произвольное
и зафиксируем его.
.
Возьмём
произвольное
и зафиксируем его.
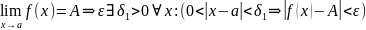
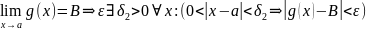
Выбираем
Модуль
разности является как угодно малой
величиной. Это означает, что выполнится
свойство
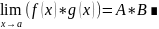
28. Предел частного функций
Если
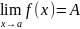 и
и
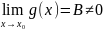 ,
то
,
то
 .
Доказательство: Можно рассматривать
как произведение функций.
.
Доказательство: Можно рассматривать
как произведение функций.
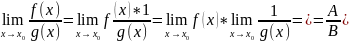 .
.
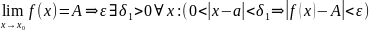

 выполняется
выполняется
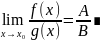
29. Теорема о пределе сложной функции
Если
функция y=f(x)
имеет
в точке а конечный предел в некоторой
проколотой окрестности точки а (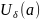 ),
а функция g(x)
имеет
в точке b
конечный
предел С, то сложная функция g(f(x))
имеет
в точке а предел С.
),
а функция g(x)
имеет
в точке b
конечный
предел С, то сложная функция g(f(x))
имеет
в точке а предел С.
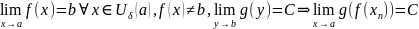
Доказательство:
Т.к.
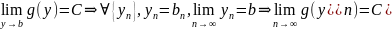
Аналогично,
т.к.

Возьмём
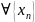 ,
,
 ,
.
Все члены этой последовательности,
начиная с некоторого номера, попадут
,
.
Все члены этой последовательности,
начиная с некоторого номера, попадут
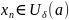 ,
где значение
фигурирует
в условии теоремы, тогда для данной
последовательности
все члены
последовательности
,
где значение
фигурирует
в условии теоремы, тогда для данной
последовательности
все члены
последовательности
 ,
будут
отличны от b.
В результате мы получаем, что для
,
будут
отличны от b.
В результате мы получаем, что для