10. Сформулировать и доказать теорему о пределе «зажатой» последовательности

Пусть числовые последовательности и , удовлетворяют условию (*). Тогда если последовательности и сходятся к одному и тому же пределу, то и последовательность сходится, причём к тому же пределу. ; .

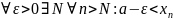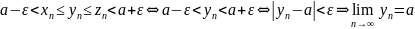Доказательство: Возьмём произвольное значение и зафиксируем его. Т.к. (**). Аналогично (***). Если взять номер N=max{ }, то мы получим, что (**). (по определению)

11. Бесконечно большие и бесконечно малые последовательности.

Опр.ббп) Последовательность 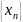называется бб, если её предел последовательности = . –ббп .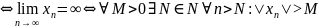

Опр.бмп) Последовательность называется бм, если её предел последовательности = . –бмп .

Теор.8) Пусть последовательности и 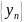являются бмп. Тогда последовательности , , 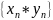, C ,C также являются бмп. Доказательство: Докажем, что –бмп. Возьмём произвольное и зафиксируем его. Т.к. –бмп, то 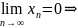для . Аналогично, –бмп, то 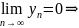для . В результате .

11. Теорема о произведении ограниченной последовательности на бесконечно малую

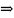
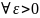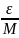
Пусть последовательность – ограниченная, а – бмп. Тогда – бмп. Доказательство: Т.к. – ограниченная . Т.к. – бмп , а значит и для 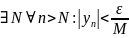. В результате получаем, что 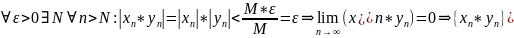–бмп.

11. Теорема о связи членов сходящейся последовательности со своим пределом и бесконечно малой.

Последовательность сходится к пределу а тттк существует бм , такая, что . Доказательство: ) Пусть . Рассмотрим последовательность =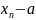 . Т.к. –бмп. 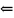) Пусть и . Докажем, что . Т.к. .

11. Теорема об арифметических операциях со сходящимися последовательностями.

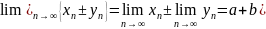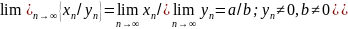Пусть и сходящиеся последовательности к а и b соответственно. Тогда: 1) ; 2) ; 3) ; 4) . Доказательство: 1) Т.к. . Последнее 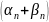– бмп (как сумма 2х бесконечно малых) 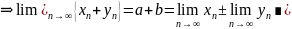2) Т.к. . Последовательности – бмп, т.е. их сумма тоже бмп.

15. Определение точных верхней и нижней граней числовых множеств. Теорема о существовании точных граней ограниченных числовых множеств.

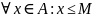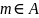Пусть A R, А – непустое числовое множество. Опр) Элемент называется максимальным элементом множества А и обозначается символом maxA или maxX(x A), когда х пробегает все элементы множества А, если: 1) ; 2) . Опр) Элемент называется максимальным элементом множества А и обозначается символом minA или minX(x A), когда х пробегает все элементы множества А, если: 1) ; 2) . Понятия мин и макс не всегда адекватно отражают понятия крайних элементов.

Множество A R называется ограниченным сверху(снизу), если существует элемент  такой, что  ( ) , при этом число M называется верхней (нижней) гранью множества A. Множество A R называется ограниченным, если существует такое, что выполнено . Всякое ограниченное сверху множество A R имеет точную верхнюю грань. Множество А не ограничено, если для любой постоянной найдется число такое, что >M.

Наименьшее из чисел, ограничивающих множество А сверху, называется точной верхней гранью. Наибольшее из чисел, ограничивающих множество А снизу, называется точной нижней гранью. Обозначения: -точная верхняя грань; -точная нижняя грань. На «языке» неравенств последнее определение записывается так: Число является точной верхней (нижней) гранью множества, если: 1) выполнено ( ); 2) такое, что ( ).

Теорема о существовании точной верхней/нижней грани.

Теорема: У любого непустого ограниченного сверху множества существует ТВГ.

Док-во: Пусть b – верхняя грань множества E, a E.

а (a+b)/2 b

[a,b] имеет непустое пересечение с множеством Е.

Свойства [a,b]: 1)⩝x E x<=b; 2)E [a,b]

Эти процедуры повторяем много раз и получаем последовательность вложенных отрезков со свойствами: ⩝x Ex<=b_k ;E [a_k,b_k]

Далее доказываем по индукции: Пусть построен отрезок [a,b] со свойствами 1 и 2. Делим его пополам соответственно [a_k+1,b_k+1] будет правым отрезком со свойствами 1 и 2. Рассмотрим длины этих отрезков b_k-a_k= . Длины эти стремятся к 0. То есть чем к>тем длина меньше. По этому существует одно единственное число общее для всех этих отрезков. Оно будет ТВГ данного множества ⩝x E:x<=c. Предположим обратное: пусть x E, x>c =>b_n-c b_n-a_n<x-c |=>b_n<x. Получили противоречие с условием

Теорема: У любого непустого ограниченного снизу множества существует ТНГ.

Док-во: Пусть a – нижняя грань множества E, a E.

а (a+b)/2 b

[a,b] имеет непустое пересечение с множеством Е.

Свойства [a,b]: 1)⩝x E x>=a; 2) E [a,b]

Эти процедуры повторяем много раз и полуаем последовательность вложенных отрезков со свойствами: ⩝x Ex>=a_k ;E [a_k,b_k]

Далее доказываем по индукции: Пусть построен отрезок [a,b] со свойствами 1 и 2. Делим его пополам соответственно [a_k+1,b_k+1] будет правым отрезком со свойствами 1 и 2. Рассмотрим длины этих отрезков b_k-a_k= . Длины эти стремятся к 0. То есть чем к> тем длина меньше. Поэтому существует одно единственное число общее для всех этих отрезков. Оно будет ТНГ данного множества ⩝x E :x>=c. Предположим обратное: пусть x E, x<c⇒b_n-c b_n-a_n<x-c⇒a_n<x. Получили противоречие с условием