Типы отображений. Обратимость отображения.
Пусть
задано отображение f:
.
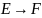Оно называется:
- инъективным (или инъекцией),
если
,
или
если уравнение f(x)
= y имеет
не более одного решения;
- сюръективным (или сюръекцией,
или отображением
множества E на F),
если f(E)= F и
если
уравнение f(x)
= y имеет
по крайней мере одно решение;
- биективным (или биекцией,
или взаимно
однозначным отображением множества E на
F),
если оно инъективно и сюръективно, или
если уравнение f(x)
= y имеет
одно и только одно решение.
Пусть
f:E
и
.
Поскольку
,
то отображение g каждому
элементу f(x)
f (E)
относит
определенный элемент 
.
Таким образом, каждому 
посредством
правила 
поставлен
в соответствие элемент
.
Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.
Пусть f:E
-
биективное отображение и F ={y}.
В силу биективности f каждому 
соответствует
единичный образ x,
который обозначим через f -1(y),
и такой, что f(x)
= y.
Таким образом, определено отображение
,
которое называется обратным
отображению f,
или обратной
функцией функции f.
Очевидно, отображение f обратно
отображению f -1.
Поэтому отображения f и f
-1 называют
взаимно
обратными.
Для них справедливы соотношения
Рассмотрим
данные понятия в алгебраической и
геометрической трактовках. Пусть задано
отображение
,
a
Y,
требуется
решить f(x)=a.
Тогда отображение f:
а) сюръективно
(f(x)=a
всегда
имеет решение, возможно не одно); б)
инъективно (не всегда имеет решение, но
если имеет, то одно); в) биективно (всегда
имеет единственное решение). Графиком
отображения
называется
множество
Числовые множества. Окрестности и их свойства.
Абсолютная
величина (модуль)
.
|x|=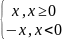
.
Свойства:
1) |x*y|=|x|*|y|;
2) |x/y/=|x|/|y| (y
0);
3) |x|
;
4) |x+y|=|x|+|y|; 5) |x-y|=
(x;y);
6) |x-y|=|y-x|. С
помощью модуля будем измерять отклонение
й величины от другой. Заметим, что |x|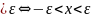
и
|x-a|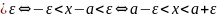
Будем
использовать следующие числовые
множества, которые называются числовыми
промежутками (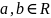
):
отрезок [a,b]:={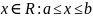
};
интервал (a;b):={
};
полуинтервал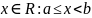 [a,b):={
}
(a,b]:={
}.
Расширенная числовая прямая. Числовая
прямая R,
дополненная двумя точками, которые
обозначаются как
и
,
называются расширенной числовой прямой
и обозначаются символом
.
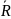Т.о.
.
Элементы
и
называются бесконечно удалёнными
точками. Если рассмотреть
как числовое множество, то
и
называются бесконечными числами. Числа
множества
будем называть конечными числами или
просто числами. Свойства конечных и
бесконечных чисел:
1)
;
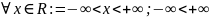2)
;
3)
;
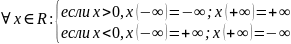4)
5)
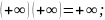
6)
.
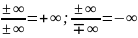Наряду
с элементами
и
рассматривают также элемент
(без
знака). Не
связана отношениями порядка с
действительными числами. Если
В
,
то B’
O’;если
A
,
то A’
O’
(поэтому
O' играет роль
)
Окрестностью
точки a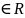
называется
любой интервал, содержащий эту точку.
-окрестностью
точки
a
называется
множество, обозначаемое
,
определяемое следующим образом
:={x:|x-a|<
}={x:a-
<x<a+
}
При
этом a
–
центр окрестности,
– её радиус. Проколотой
-окрестностью
точки
a
называется
множество
.
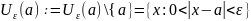Свойства окрестности: 1) если
,
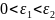то
;
2)
;
3) Свойство
отделимости Хаусдорфа:
.
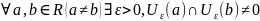Понятие
окрестности для бесконечно удалённых
точек: пусть М>0.
;
;
Понятие окрестности позволяет измерять меру отклонения точек некоторого множества от некоторой фиксированной точки. Чем меньше значение ,тем ближе точки -окрестности точки а расположены к а.