63. Формула Тейлора с остатком в форме Пеано
Пусть
-- остаток в формуле Тейлора для
функции
в точке
,
и функция
имеет непрерывную (n+1)-ю
производную. Тогда
--
бесконечно малая величина того же или
большего порядка малости, как
, при
. (Остаточный член
,
о котором известны эти сведения о порядке
малости, называется остаточным
членом в форме Пеано.)
Доказательство.
Утверждение теоремы означает, что
существует
При
остаток
будет иметь тот же порядок малости, что
,
а при L=0 -- больший порядок малости.
Итак, вычислим предел:
Применим
к этому пределу правило Лопиталя,
повторив этот приём n раз:
|
|
|
|
|
|
.Последний
предел мы вычислили прямой подстановкой,
поскольку по предположению
--
непрерывная функция. Существование
предела доказывает утверждение теоремы.
64. Единственность формулы Тейлора
Формула Тейлора
Теорема 2. (Единственность представления функции по формуле Тейлора) Если f имеет n–ю производную в точке и
,
то
.
Лемма.
Если
(2)
то
=0,
k=0,1,…,n
Доказательство.
в (2) перейдем к пределу при x
, получим
= 0,
,
делим полученное выражение на (x-
)
и переходим к пределу при x
и т.д.
Доказательство теоремы.
откуда и следует утверждение.
65. Формула Тейлора с остатком в форме Лагранжа
Если f(x)
n+1 раз
дифференцируема в окрестности точки
,
то
f(x)=f(
)=f’(
)(x-
)+
,
где х –
некоторая точка из указанной окрестности,
а
– точка,
лежащая строго между
и x.
Доказательство:
Пусть
– остаточный член. Он удовлетворяет
условию:
.
Рассмотрим функцию
,
хотя в точке
будет
удовлетворять тем же условиям.
.
Пусть для определенности
,
тогда
,
где точка
лежит строго между
и
,
а значит между
.
В результате
получаем, что
66. Теорема о необходимых и достаточных условиях возрастания и убывания дифференцируемой функции.
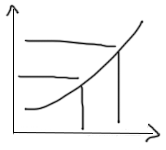
Функция
f(x)
называется
возрастающей на (a;b),
если
.
Теорема)
Функция f(x):
(a;b)
,
дифференцируемая
на этом промежутке, обладает следующими
свойствами:
;
;
;
Доказательство:
Докажем п2) остальное аналогично. (1)Пусть
.
Возьмём произвольные точки
и
,
такие,
что
.
Согласно
т. Лагранжа
.
(2)Пусть f
,
.
Точку
можно
представить как
,
где
.
Тогда
67. Необходимое условие существования экстремума.
Теор) Если в точке непрерывная f(x) достигает экстремума, то в этой точке её производная или =0, или не существует. Доказательство: Пусть точка является экстремальной точкой. Тогда в этой точке возможны только 3 условия:
;
не существует.
Если выполняется 1 случай, то f(x) в окрестности этой точки, согласно теореме о необходимых и достаточных условиях возрастания и убывания функции, является либо возрастающей, либо убывающей и экстремума в этой точке быть не может. Значит, остается 2 и 3 случай и теорема доказана
Точки, в которых производная , называются стационарными точками; в которой производная =0 или не существует называются критическими или подозрительными на экстремумы.
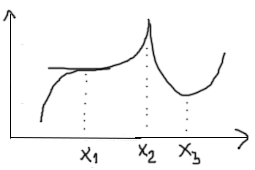
–стационарная;
,
,
–критические,
при этом
,
–экстремальные
точки,
-нет.