59. Теорема Ролля и её геометрический смысл
Пусть
f(x)
непрерывна
на [a;b],
дифференцируема в (a;b) и
на концах отрезка принимает одинаковые
значения, т.е. f(a)=f(b).
Тогда
найдётся хотя бы одна точка
,
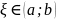такая, что
.
Доказательство: Т.к. f
является
непрерывной на [a;b],
то найдётся
точка на отрезке [a;b],
в которой f(x)
принимает своё наименьшее m
и наибольшее
M
значения.
Если m=M,
то f(x)
на [a;b]
является постоянной, а знафит её
производная на этом отрезке = 0, и в
качестве точки
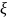можно выбрать любую точку этого отрезка.
Пусть
,
тогда имеет место по крайней мере 1 из
вариантов (или оба): а) f(x)=f(b)>m;
б) f(a)=f(b)<M.
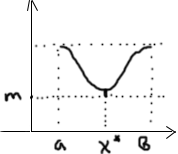
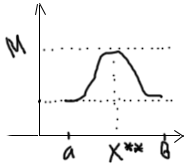
Это
означает, что
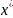и
является экстремальными точками и по
теореме Ферма производная в этих точках
=0, а значит в качестве
можно взять эти точки. Прим) точка
возможно не единственна
60. Теорема Лагранжа о конечных приращениях и геометрический смысл.
Если f(x)
непрерывна
на [a;b]
и
дифференцируема
в (a;b), то
найдётся точка
такая, что
f(b)-f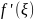(a)=
(b-a)
Доказательство:
Рассмотрим вспомогательную функцию
F(x)=f(x)-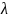
x.
Значение
выберем
из условия F(a)=F(b).
Тогда
F(a)=f(a)-
a,
F(b)=f(b)-
b
.
F(x) удовлетворяет
всем условиям теоремы Ролля. Она
непрерывна на [a;b],
дифференцируема в (a;b) и при выбранном
значении
F(a)=F(b). Значит,
существует точка
,
такая, что
Точка возможно не единственная.
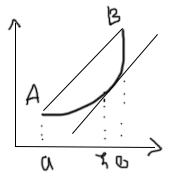
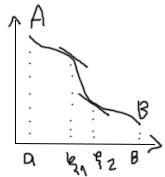
Геометрический смысл теоремы в том, что найдётся точка , в которой касательная к графику f(x) будет параллельна хорде, соединяющей точку A(a;f(a)) и B(b;f(b))
Теорему
часто записывают в следующем виде
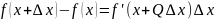(формула конечных разностей, которая
дает точное значение приращения функции
в точке)
61. Теорема Коши.
Если f(x)
и g(x)
непрерывны
на [a;b],
дифференцированы
в (a;b)
и производная g’(x)
0
на интервале
(a;b),
то существует точка
, такая, что
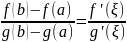(1)
Доказательство:
Если g’(x)
0,
то g(b)
g(a).
Рассмотрим
вспомогательную функцию F(x)=f(x)-
g(x).
Значение
выберем
из условия F(a)=F(b),
тогда f(b)-
g(b)=
f(a)-
g(a)
.
F(x) при
выбранном значении
удовлетворяет
всем условиям теоремы Ролля, а значит
найдётся такая точка
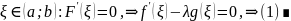
62. Правило Лопиталя раскрытия неопределенностей 0/0 и ∞/∞
Пусть
функции f(x)
и g(x)
дифференцируемы в некоторой окрестности
точки a,
за исключением, быть может, самой точки
a,
и пусть
или
.
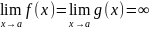Тогда, если существует предел отношения
производных этих функций
,
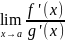то существует и предел отношения самих
функций f(x)/g(x)
при x→а,
причем
.
Таким
образом, коротко правило Лопиталя можно
сформулировать следующим образом:
предел отношения двух бесконечно малых
или двух бесконечно больших величин
равен пределу отношения их производных.
Доказательство:
Мы ограничимся случаем, когда а-нечётное
число и функции f(x)
и g(x)
являются
бм. Т.е. мы имеем неопределенность
.
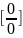Т.к. по условию теоремы f,g
.
Доопределим
f и
g
в a,
так, чтобы
они стали непрерывными. Полагая
f(a)=g(a)=0,
тогда
.
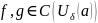Тогда
по
следствию т. Коши найдётся такая точка
,
что
,
причём точка
будет лежать строго между a
и x.
Из неравенства
0<|a-
|<|a+x|
и геометрических соображений следует,
что когда
получаем
