44.Теорема об ограниченности непрерывной на отрезке функции

Теорема: Непрерывная на сегменте [a,b] функция ограниченна на этом сегменте

Док-во: функция ограниченна если ∃ М ∀ х ∈[a,b]: |f(x)|≤M

f(x) ограниченна на [a,b]. Функция неограниченна если ∀М ∃ х ∈[a,b]: |f(x)|>M.

Пусть ∀n∃x_n∈[a,b]: |f(x_n)|>n⇒(по теореме Больцано - Веерштрасса)

противоречие ⇒ЧТД

∃{Xn_k}→x₀ ,x∈[a,b] ⇒|f(Xn_k)|>n_k

|f(Xn_k)|→f(x₀)

45. Теорема о достижении непрерывной на отрезке функции своих точных граней Если функция f(x) непрерывна на отрезке [a;b], то найдутся точки , принадлежащие отрезку [a;b], в которых функция f(x) достигает своих точных нижней и верхней граней.

46. Теорема о непрерывности обратной функции

Строго монотонная и непрерывная на отрезке [a;b] функции y=f(x) имеет на отрезке с концами f(a) и f(b) обратную функцию, которая также является строго монотонной с сохранением характера монотонности и непрерывности.

47. Определение и геометрическая интерпретация равномерной непрерывности. Теорема Кантора.

функция f(x) определена на Х называется равномерно непрерывной на этом множестве если ∀ ε>0 ∃δ>0 ;∀ х’ :x’’∈ Х: |x’-x’’|<f⇒|f(x’)-f(x’’)|<ε

Равномерная непрерывная функция на множестве будет непрерывной, обратное не верно. Геометрически свойство равномерности означает, что график функции f(x) не имеет неограниченно крутых участков на Х.

Теорема Кантора: ∀ непрерывная на отрезке [a,b] функция будет равномерно непрерывной на этом отрезке. Док-во: от противного. ∀ ε>0 ∃δ>0 ;∀ х’ :x’’∈ Х: |x’-x’’|<f⇒|f(x’)-f(x’’)|≥ε; для∆=1/n ∃Un,Vn: |Un=Vn|<1/n : |f(Un)-f(Vn)|≥ε₀ (1)

По теореме Больцано – Веерштрасса∃ {Un}: lim_k→∞Un_k=x₀∈[a,b] ⇒иlim_k→∞Vn_k=x₀

Так как функция непрерывна, то⇒ lim_k→∞f(Un_k)= lim_k→∞f(Vn_k)=f(x₀)⇒lim_x→∞|f(Un_k)-f(Vn_k)|=0⇒противоречие с (1)

48. Определение производной функции в точке. Односторонние производные. Примеры функций, не имеющих производных в точке.

Пусть функция f(x) определена в некоторой окрестности точки . Опр1) Производной функции f(x) в точке называется предел отношения приращения значения функции к приращению аргумента, когда последний стремится к 0, если этот предел существует и конечен. Т.о., если , то Обозначается 1 из следующих способов: y'( ), f'( ), . При этом нужно понимать, что f’( ) (f( )'. Если предел не существует или равен , то конечной производной не существует. (имеет бесконечную производную)

Опр2) Если f(x) определена в левой или правой полуокрестности точки , то можно определить одностороннюю производную

; .

Из определения предела следует, f(x) имеет в точке производную тттк правая производная = левой производной. Свойство функции иметь производную записывают как ; быть непрерывной .

49. Механический и геометрический смысл производной. Уравнение касательной и нормали к кривой.

Пусть материальная точка движется по прямой так, что каждый момент времени t известно расстояние s(t) от некоторой фиксированной точки. В этом случае говорят, что f=s(t) выражает закон движения донной материальной точки. За промежуток от момента t до t+ будет пройдено расстояние s(t+ )-s(t). Отношение называется средней скоростью данной точки, если существует конечный предел , то он называется скоростью материальной точки в момент времени t. Т.о. с механической точки зрения производная закона пути в момент времени t есть скорость мат.точки.

Для любой функции y=f(x) выражающей некоторый процесс, производная есть скорость изменения данного процесса – физический смысл.

Рассмотрим задачу о проведении касательной к плоской кривой L . Пусть её уравнение в ДСК y=f(x). Возьмём произвольную точку и точку . Предельное положение точки секущей , когда точка М по кривой L стремится к , называется касательной к кривой L в точке . Заметим, что не во всякой точке кривой существует касательная. (в точках излома и заострения)

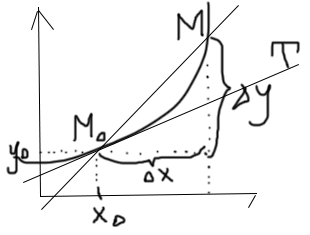
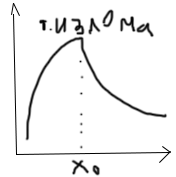
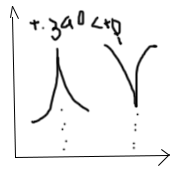
Теор) Если y=f(x) имеет в точке конечную производную, то в этой точке у неё существует касательная, уравнение которой y=f( )+f'( )(x- ). Доказательство: уравнение прямой, проходящей через точки и . ; ; ; . Замеч) Т.к. касательная геометрический объект, она существует и в тех случаях, когда «не работает».

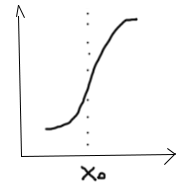
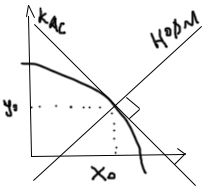
Прямая, перпендикулярная касательной в точке касания, называется нормалью к прямой. Т.к. нормаль перпендикулярна касательной, то её угловой коэффициент . Уравнение нормали имеет вид: y=f( )- *(x- )

Т.о. геометрический смысл производной заключается в том, что производная y=f(x) в точке равна tg угла наклона касательной к оси ОХ.