1. Способы задания множеств. Отношения между множествами. Операции над множествами.

Множеством называется совокупность объектов, объединенных по какому-либо признаку или условию в единое целое. Объекты, из которых состоит множество, называются элементами этого множества. И тот факт, что элемент а принадлежит множеству А записывается так 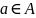(иначе 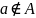). Существует множество, не содержащее ни одного элемента (обозначается ). Отбирая элементы множества, мы проводим операции над элементами более широкого множества, которое называется универсальным (обозначается U). Основные способы задания множеств.

а) А= - явное перечисление всех элементов. Недостаток – конечность количества элементов множества А.

б) Указание характеристических свойств: множество А определяется как совокупность тех и только тех элементов из некоторого множества U, которые удовлетворяют общему свойству Р. И тот факт, что элемент x обладает свойством Р, записывается так Р(х). Пишут . Если из контекста понятно, о каком универсальном множестве идёт речь, то пишут короче

Основные множества МА:

1. Натуральные числа

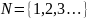
2. Натуральные числа + 0

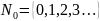
3. Целые числа

4. Рациональные числа

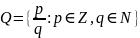
5. Действительные числа

6. Комплексные числа

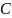
Отношения между множествами. Операции над множествами.

Пусть А и В –2 множества, образованных из элементов универсального множества U.

1. Множество А называют равным множеству В, если они состоят из одних и тех же элементов (А=В)

2. Множество А называется подмножеством множества В, если каждый элемент множества А является элементов множества В( )

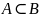3. Имея множества А и В, мы можем образовывать новые множества с помощью следующих операций:

1. Объединение А и В – множество, состоящее из элементов, принадлежащих А или В ( )

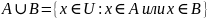2. Пересечение А и В – множество, элементы которого одновременно принадлежат А и В ( )

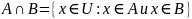3. Разность А и В – множество, состоящее из тех элементов А, которые не принадлежат В ( )

4. Дополнение множества А (до универсального множества U) – множество, элементы которого не являются элементами множества А. Обозначается

5. Декартовым произведением А и В называется множество упорядоченных пар (a;b), где a 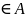, b ( )

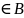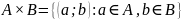2. Символы математической логики.

Для придания точности формулировкам в МА широко используются символы мат. логики. При этом утверждения становятся более короткими и выразительными. Пусть p и q – некоторые высказывания(утверждения), т.е. предложения, относительно которых можно сказать, что они истинны или ложны. Запись p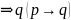 означает, что из высказывания p следует высказывание q (p - посылка, q - заключение). Сам символ называется импликантой. Запись p читается как p эквивалентно q, символ эквивалентности. Широко используются символы, называемые кванторами: – квантор всеобщности (All), 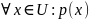– для любого х из множества U выполняется утверждение р; 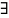– квантор существования (Exist), – существует х из множества U, для которого выполняется утверждение р. 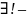существует единственный элемент. Запись p:=q означает, что p по определению = q, при этом подразумевается, что p более компактная форма, чем q. Запись 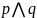называется конъюнкцией утверждений p и q. Истинна тттк истинны оба высказывания, 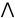– символ конъюнкции. Запись 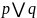называется дизъюнкцией утверждений p и q. Истинна тттк истинно хотя бы одно из высказываний, – символ дизъюнкции. Запись 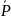– отрицание Р. Если Р истинно, то ложно и наоборот. Вместо символа конъюнкции запись (p,q,v) z означает, что если использовать 3 утверждения в скобках, то будет истинно z. Можно записать в форме таблиц истинности. (таблица + теоремы)