14. Политропа с постоянным и переменным показателем. Показатели политропы.

Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела, подчиняющийся уравнению, которое может быть представлено в следующих формах:

; ; = .

где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (-  n  +).

Физический смысл показателя политропы п определяется после дифференцирования выражения .

Из соотношения непосредственно следует .

Это значит, что постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах. Значения этих работ могут быть определены графически в координатах (рис. 6а).

В логарифмических координатах политропный процесс (политропа) с постоянным показателем представляет собой прямую линию (рис. 6б)

.

Постоянный показатель политропы определяется как тангенс угла наклона линии процесса к оси абсцисс ( ) (рис. 6б)

n = = .

а б

Рис. 6. Политропа с постоянным показателем

для изобарного процесса n = 0, для изохорного процесса - n = ± ∞,

для изопотенциального процесса - n = 1 (рис. 7).

Расчет политропного процесса с переменным показателем вызывает необходимость ввести в рассмотрение три показателя процесса: истинный показатель процесса (n); первый средний показатель и второй средний показатель (m).

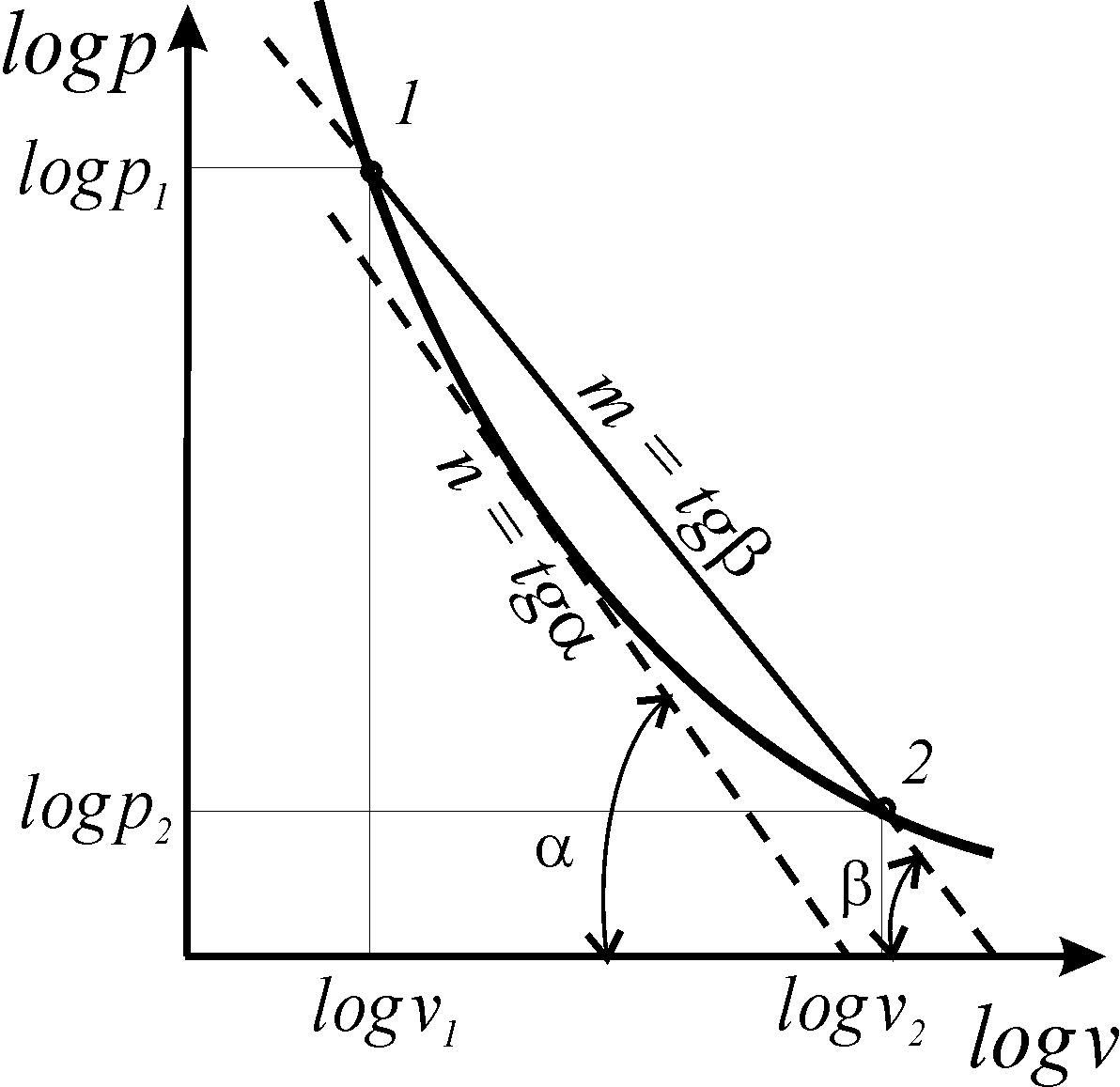
Рис. 8. Политропа с переменным показателем

Истинный показатель процесса (n) определяется как соотношение элементарной потенциальной работы к элементарной термодинамической работе , что соответствует тангенсу угла наклона касательной, проведенной к кривой процесса в точке процесса, к оси абсцисс ( ) в логарифмической сетке координат

n = = tg.

Истинный показатель политропы определяется соотношением .

Первый средний показатель политропы .

Второй средний показатель политропы численно равен тангенсу угла наклона секущей 1-2 к оси абсцисс ( ) в логарифмической сетке координат (рис. 8)

m = = .

Непосредственно из последнего выражения (98) следует уравнение политропы с переменным показателем

.

15. Работа в термодинамических процессах простых тел.

Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах можно получить при сопоставлении их элементарных значений: ;  .

Соотношение для определения удельной термодинамической работы в конечном процессе (1-2)

.

Зависимости для определения удельной термодинамической и потенциальной работы в конечном процессе примут следующий вид:

; .

Соотношение для определения характеристики расширения или сжатия в рассматриваемом процессе имеет следующий вид:

= = .