Виды статистических гипотез

Гипотеза о долях	для дихотомических переменных (имеют два значения: да или нет)	гипотеза для 1-ой совокупности
		гипотеза для 2-х совокупностей
	для недихотомических переменных (имеют множество значений)	для 1-й совокупности
		для 2-х совокупностей
Гипотеза о средних	для 1-й совокупности
	для 2-х совокупностей	Случай с равными дисперсиями
		Случай с неравными дисперсиями
Гипотеза о дисперсиях	для 2-х независимых совокупностей
	для 2-х зависимых совокупностей

В случае 1-й совокупности утверждение нулевой гипотезы формулируется как равенство неизвестного параметра некоторому числу (константе):

H₀: p = const

H₁: p ≠ const

В случае 2-х совокупностей утверждение нулевой гипотезы формулируется как равенство параметров двух совокупностей:

H₀: µ₁ = µ₂

H₁: µ₁ ≠ µ₂

В реальных исследованиях изучается одна ВС, которая затем делится на непересекающиеся группы (по полу; возрасту; доходу и так далее) и ставится задача определить наличие различий в двух выделенных совокупностях по любому основанию.

p – доля положительных ответов на выборку.

Сравнение доли положительных ответов 2-х выборок: ,

Совокупности называются независимыми тогда, когда элементы 1-й совокупности не могут оказаться элементами другой совокупности (пол, возраст). Совокупности называются зависимыми когда элементы 1-й совокупности могут быть элементами другой совокупности (1 и та же группа респондентов, но в разные промежутки времени).

Гипотеза о долях для дихотомической переменной

а) ГоДдДП для одной совокупности проверяется Н₀ о равенстве доли положительных значений признака некоторому числу:

H₂: p > const

H₃: p < const

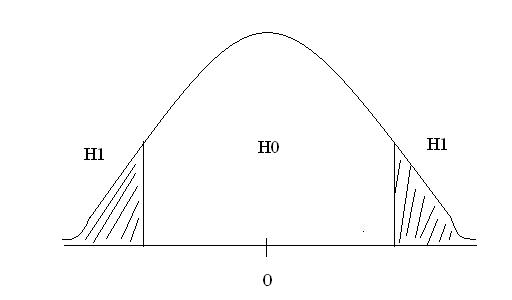
Альтернативная Гипотеза, сформулированная со знаком неравенства, говорит о том, что параметр ГС не совпадает с константой. …со знаком «больше» говорит о том, что параметр ГС больше константы; …со знаком «меньше» … меньше константы. Знак неравенства как альтернативная гипотеза в любом случае, но не определим направления; Знак больше мы можем использовать в АГ, если статистика, полученная в результате выборочного исследования больше константы. Знак меньше … меньше константы. В основе построения статистического критерия лежит СНР:

Формула критерия: 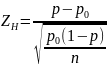; p₀ = const.

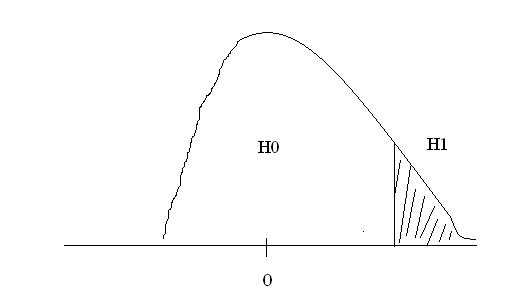
Решение о подтверждении или опровержении Н₀ принимаем исходя из того, в какую область попадет Z_H (статистика критерия), если в середину распределения принимаем нулевую гипотезу, если в хвост распределения (критическую область), то Н₀ отвергается в пользу альтернативной.

Гипотеза о долях для дихотомической переменной в случае 2-х совокупностей.

В основе построения статистического критерия лежит СНР.

Гипотезы о долях для недихотомической переменной

Только номинальные и порядковые переменные. Для НДП проверяется нулевая гипотеза о равенстве распределений. В случае формулировки гипотезы для 1-й совокупности проверяется равенство распределения ГС некоторому теоретическому распределению. В случае формулировки проверки Н₀ для 2-х совокупностей проверяется равенство распределений определенного признака 2-х изучаемых ГС. В основе построения статистических критериев проверки гипотезы для НДП лежит теоретическое распределение х² (хи квадрат). Критическая точка для проверки гипотезы определяется по статистической таблице х² на основе 2-х параметров:

- α – уровень значимости;

- df - число степеней свободы.

Ккр = x²_1-α;df df = k – 1, где k – количество значений признака.

.

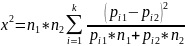Все значения точек положительные.

Гипотезы о средних

Для одной совокупности проверяется Н₀ о равенстве среднего ГС (математического ожидания) некоторому числу (константе):

H₀: µ = µ₀(const).

Н₁ может быть сформулирована со знаками < или >. Направленная Н₁ формулируется со знаком < или > в зависимости от того, < или > вычисленная в выборке исследуемая статистика по отношению к константе. В основе построения статистического критерия лежит теоретическое распределение Т-Стьюдента. Для того чтобы найти Ккр, используется статистическая таблица Т-Стьюдента:

Ккр = t_1-α;df df = n.

Гипотеза о средних для 2-х совокупностей. Формула Н₀, утверждает, что среднее для ГС (МО) одной совокупности совпадает с МО второй совокупности.

В основе построения критерия лежит статистическое распределение Т-Стьюдента. Рассмотрим два случая проверки гипотезы о средних для двух совокупностей:

1) для равных дисперсий: Ккр = t_{1- б; df} df = n₁ + n₂ – 2

2) дисперсии не равны:

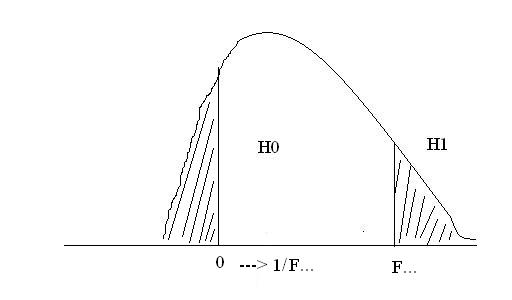
Гипотеза о дисперсиях

1) независимые совокупности;

2) зависимые совокупности;

Замечание: в социологии гипотезы о равенстве дисперсий рассматриваются, как правило, для того чтобы ответить на вопрос, равны ли дисперсии 2-х совокупностей. В зависимости от вывода проверяется основная гипотеза о равенстве средних, поэтому в социологии рассматривается гипотеза о равенстве дисперсий двух независимых совокупностей.

Н₀ утверждает, что дисперсии 2-х независимой совокупности совпадают. Н₁ утверждает обратное. Направленная гипотеза не рассматривается. H₀: ϭ₁ = ϭ₂ H₁: ϭ₁ ≠ ϭ₂

В основе построения статистического критерия лежит Т-Распределение Фишера:

df₁ = n₁ - 1 df₂ = n₂ - 1