Характеристика центра распределения признака (меры центральной тенденции)

Являются 3 показателя:

- Мода (М_о);

- Медиана (М_е);

- Среднее арифметическое.

Мода – значение признака, обладающее наибольшей частотой. Мода может быть определена для любых измерительных шкал.

Для качественных признаков и количественных, не сгруппированных в интервалы, Мода определяется по частотному распределению.

Если количественный признак сгруппирован в интервалы, мода может определяться двумя способами:

1) графический (по гистограмме) (стаж руководителей);

М интервал - интервал, которому соответствует м частота.

2) используя формулу:

Х₀ - нижняя граница МИ;

l - длина МИ;

FМо - частота в %, соответствующая МИ;

f^- - частота в %, соответствующая предшествующему И;

f⁺ - частота в %, соответствующая последующему И.

Пример интерпретации: чаще всего среди студентов 1-го курса встречается возраст 18 лет.

Медиана – значение признака, которая делит упорядоченный ряд данных пополам таким образом, что число единиц наблюдения с большим и меньшим, чем медиана, значением признака, одинаково; 50-ый процентиль.

X₀ – левая граница МИ;

l – длина МИ;

F – предшествующая накопленная частота;

f_Me - частота в %, соответствующая МИ.

Так как номинальная шкала не обладает свойством упорядоченности/порядка, мы не можем определить (Ме). Для остальных определяется. Для порядковых шкал и количественных признаков, представленных в виде вариационного ряда, медиана определяется приблизительно по возрастающей накопленной частоте. В медиане будет соответствовать возрастающая накопленная частота, равная либо впервые превысившая 50%. Если количественный признак сгруппирован в интервалы, точное значение медианы можно найти по формуле внутри медианного интервала. Медианный интервал - интервал, для которого возрастающая частота равна либо впервые превысила 50%. Пример интерпретации: половина студентов имеют возраст до 18 лет, вторая половина – после 18 лет.

Среднее арифметическое – сумма всех значений признака, делённая на объём ВС.

Вычисляется только для количественных признаков. В зависимости от того, как представлен количественный признак, используется своя разновидность:

1) сырые данные: ;

2) вариационный ряд: ; x_i и f_i – значение признака и соответствующая абсолютная частота;

3) группировка в интервалы: ; – середина интервала.

Пример интерпретации: средний возраст составляет 17,8 лет.

Показатели вариации признака.

Вариация – различие в значениях какого-либо признака у разных единиц изучаемой совокупности. Всегда связана с такой характеристикой центра распределения, как среднее арифметическое. (Вариация) и её показатели определяются только для количественных признаков. Чем больше отдельное значение различается между собой, тем больше они отличаются от СА и наоборот (чем меньше…). Если распределение количественного признака характеризовать только с помощью СА, мы получим информацию только о некой типичной или характерной величине, однако строение совокупности нам будет неизвестно.

Для того чтобы представлять значение совокупности, вводятся специальные показатели, которые численно характеризуют отклонения отдельных значений от СА.

Предположим, обследуются 2 группы семьи из количества детей.

1. 0 6 3 1 5 = 3

2. 4 2 3 3 3 = 3

d1 = 6 - 0 = 6

d2 = 4 - 2 = 4

К показателям вариации относятся:

1) d размах - разница между максимальным и минимальным (показателем признака). Однако показывает лишь крайние отклонения значений признака и не отражает отклонений всех вариантов в ряду.

2) S² дисперсия - представляет собой средний квадрат отклонений значений признака от СА. В зависимости от того, в каком виде представлены исходные данные, дисперсия вычисляется по соответствующей формуле:

1) сырые данные: ;

2) вариационный ряд: ;

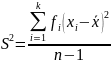3) интервалы: .

В знаменателе вычитание единицы производится тогда, когда объём выборочной совокупности n меньше 50. Если n > 50, вычитать 1 не обязательно. Вычитание – поправка на малый объём выборочной совокупности. Это очень важный показатель вариации, однако он используется редко, так как трудно интерпретируется.

3) S среднеквадратическое отклонение (СКО; стандартное отклонение) Std, deviation. - корень квадратный из дисперсии. Отличительная особенность - показатель измеряется в тех же единицах, что и значение признака, поэтому он может интерпретироваться.

3 формулы вычисления такие же, как и у дисперсии, только из значения нужно извлечь корень ( ). Пример интерпретации: возраст студентов 1-го курса в среднем отклоняется на 1,9 года от = 17,8 лет.

4) V коэффициент вариаций – выраженное в процентах отношение СКО к СА, используется для сравнительной оценки вариаций в различных количественных признаках, в различных совокупностях. Используется как характеристика однородности изучаемой совокупности по конкретному признаку. Совокупность считается однородной по данному признаку, если для него коэффициент вариаций не превышает 33%.

Извините, в моей тетради этой темы нет, и соответсвенно, нет формул.

Дополнительные меры вариации:

1) показатель отклонения признака вокруг медианы;

2) интерквартильный диапазон от 25 процентиля до 75 процентиля; - интервал, в котором вокруг медианы сосредоточились 50% ответов респондента. Используется, когда в качестве характеристики центра распределения нельзя использовать СА. (Для порядковых шкал и в случае большой ассиметрии);

3) меры качественной вариации; меры вариации, измеренные по номинальных шкалам и приведенных к дихотомическому виду. Такая мера характеризует степень отклонения распределения признака от равномерного, то есть, когда каждому значению признака соответствует одно и то же число объектов. Тогда максимальное значение меры качественной вариации соответствует ситуация равномерного распределения, а минимальная ситуации, когда все объекты сосредоточены в одном значении признака.

Анализ формы распределения количественного признака.

1. ФРКП может анализироваться 2-мя способами:

1) графический. Предполагается, что данные сгруппированы в интервалы равной длины, причем длина интервала стремится к 0. Тогда, если по гистограмме для данного представления построить полигон распределения, можно предположить, что ломаная прямая полигона преобразуется в плавную кривую. (1) Тогда процедура формы эмпирического распределения представляет собой сравнение эмпирической кривой распределения с теоретической кривой нормального распределения;

2) аналитический. Сравнение между собой характеристики центра распределения и показатели нумерации.

Способы равноправны.

Характеристики ФЭР являются:

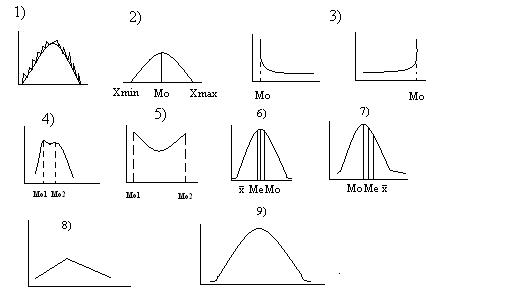
1) модальность. По числу и характеру мод:

- одномодальные - распределения с одним ярко выраженным значением признака (с 1 модой):

- колоколообразные Xmin<Mo<Xmax (2). Мо не является крайним значением;

- j-образные Мо совпадает с Xmin или Xmax (3);

- полимодальные - наличие 2-х и более модальных значений. Наиболее распространенная форма - бимодальность: показывает, что изучаемая совокупность неоднородна по данному признаку.

Если мы встречаем бимодальность, то необходимо сначала определить причину бимодальности, затем изучать распределения данного признака для определения 2-х совокупностей. В крайнем случае бимодальности является так называемое U-распределение: Mo₁ = Xmin, Mo₂=Xmax (5). Наличие такого распределение говорит о крайней поляризации мнений.

2) симметричность:

- симметричные характеризуется совпадением характеристик центра распределения; Мода совпадает с медианой и СА:

- ассиметричные ;

- с левосторонней асимметрией (отрицательная асимметрия). Наличие длинного левого хвоста распределения; (6)

- с правосторонней асимметрией (положительная (асимметрия). Колокол с длинным правым хвостом. (7)

Для сравнительного анализа степени асимметрии рассматривается относительный показатель асимметрии: ;

3) протяженность (эксцесс);

В зависимости большой или малой дисперсии (СКО) распределение может быть сплощенным (платокритическим);

Чем меньше дисперсия, тем более выпуклая будет форма распределения - лептокритическое распределение.

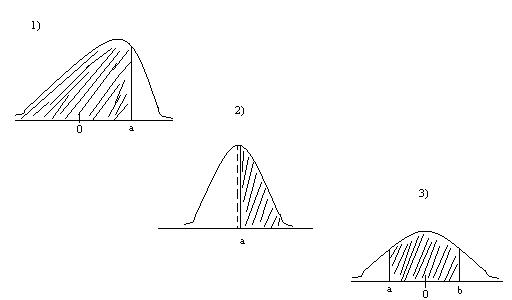
1) Вероятность Р – вероятность того, что случайная величина х попадёт в заштрихованную область = F(a). P(x<a) = F(a).

2) P(x>a) = 1 – F(a).

3) P(xЄab) = F(b) – F(a); a<x<b.