Графическое представление данных

Графики предназначены для более наглядного представления результатов исследования, а также для более детального и глубокого анализа полученных данных. Виды графиков (будем изучать):

1) круговая диаграмма;

2) диаграмма полос и/или столбцов;

3) ленточная диаграмма;

4) гистограмма;

5) полигон распределения;

6) графики накопленных частот;

7) график интерквартильного диапазона.

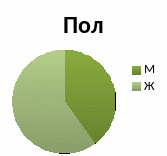
1) Круговая диаграмма применяется для изображения распределения качественных признаков. На круговой диаграмме частоты представляются в виде площадей-секторов. Для того чтобы определить искомую площадь сектора необходимо вычислить пропорцию

360^о - 100%.

х - f_i(%).

x = 360*f_i(%)/100%.

Нулевой градус – ???

После того как сектора обозначены, необходимо выделить каждый сектор либо цветом, либо штриховкой. Любая диаграмма должна иметь заголовок и легенду.

Пол	fi(%)
М Ж	40% 60%

2) используется для представления качественных признаков.

Представляет собой набор прямоугольников с равными основаниями и расположенными на одинаковом расстоянии друг от друга. Высота прямоугольника зависит от частоты. Каждый прямоугольник представляет собой отдельное значение признака. В ДС основания располагаются по оси Х, а соответствующие частоты по оси У. В ДП основания прямоугольников располагаются по оси У, а частоты по оси Х.

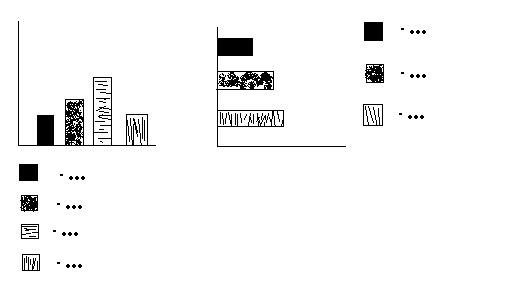
3) применяется для всех видов измерительных шкал и предназначена для изображения структуры распределения. Представляет собой полоску, длина которой равна 100%. Полоска делится на доли (сектора) в соответствии с частотой того или иного значения.

Ленточная диаграмма наиболее эффективна в сравнительном контексте. Для примера приведем динамику распределения лиц с ВО по году.

4) Применяется для количественных признаков, группированных в интервалы. По оси Х откладываются интервалы, по оси У - соответствующие частоты.

Набор прямоугольников, плотно прилегающих друг к другу. Служит для изучения формы распределения количественного признака.

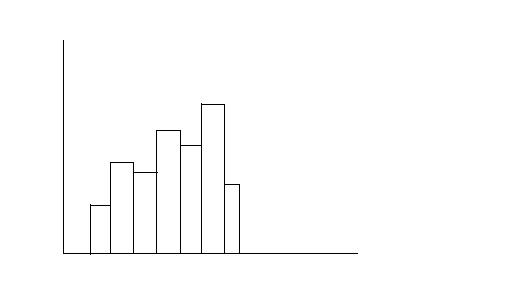
Не требует выделение разным цветом либо штриховкой различных прямоугольников.

Если гистограмма строится по аналитической группировке, то есть, длины интервалов одинаковые, по оси У откладывается соответствующая частота. Если гистограмма строится по типологической либо процентивной группировке, то есть, длины интервалов разные, по оси У откладывается не частота, а плотность распределения.

5) Строится для количественных признаков.

Ломаная линия, строящаяся так: по оси Х откладываются единичные значения признака. По оси Х соответствующие этим значениям частоты. Затем эти точки соединяются.

Если число значений признак небольшое, в этом случае полигон строится для конкретных значений. Если же число значений признака большое (вариационный ряд длинный), лучше строить для сгруппированных данных. В этом случае в качестве значения признака используют середину каждого интеравала. Если ПР нужно построить для сгруппированных данных, то его совмещают с гистограммой.

Если ПР совмещается с гистограммой, то он, как и гистограмма, используется для визуализации и дальнейшего изучения форм распределения признака.

6) 2 вида графиков:

- кумулята - график, построенный по абсолютным значениям накопленных частот.

- огива - по накопленной частоте в процентах

Строятся для всех измерительных шкал, для которых имеет смысл расчет НЧ.

По оси Х - значение признака, по оси У - значения НЧ.

На одном и том же графике могут присутствовать одновременно кривая, построенная пои возрастающей НЧ, и кривая, построенная по убывающей НЧ. Графики НЧ можно строить для данных, сгруппированных в интервалы. В этом случае кривая, отстроенная по возрастающей НЧ в качестве значения признака использует верхнюю или правую границу интервала. По убывающей НЧ - нижняя или левая граница интервала.

7. Это разность между квантилем Х_0,75 и Х_0,25

График ИД имеет только 1 измерение (шкала значений признака) и строится по 5 точкам Хmin, Х_0,25, Х_0,5, Х_0,75 и Хmax.