Частотная модель парных связей. Таблицы сопряженности.

Статистическая связь между двумя признаками изучается с помощью таблиц сопряженности. Если мы хотим поместить в таблицу сопряженности количественный признак, его необходимо преобразовать в «качественный» вид с помощью группировки в интервалы (типологический). Таблица сопряженности предназначена для изучения совместного частотного распределения двух качественных признаков. Построив таблицы сопряженности, мы можем ответить на вопросы:

- как 1 признак распределяется относительно другого (меняется ли частотное распределение одного признака);

- есть ли статистическая связь между изучаемыми признаками;

- чему равна мера (коэффициент) связи (имеет смысл тогда, когда статистическая связь присутствует).

Таблица сопряженности состоит из нескольких структурных элементов:

- строка и столбец заголовка (верхняя строка и крайний левый столбец содержат значения признаков, для которых строится таблица сопряженности);

- внутренние ячейки (образовываются при пересечении строк и столбцов и содержат информацию о совместных частотных распределениях первого и второго признака);

- маргинальная строка и маргинальный столбец (нижняя строка и крайний правый столбец содержат одномерное частотное распределение изучаемых признаков);

- ячейка, образованная при пересечении маргинальной строки и маргинального столбца и содержащая информацию об объёме выборочной совокупности.

Общий вид таблицы сопряженности:

II I пр пр	X1	X2	…X3…	Xc
Y1	f1i	f12	…f1j…	f1c	fi0
Y2	f2i	f22	…f2j…	f2c	f20
… Yj …	… fi1 …	… fi2 …	… …fij… …	… fic …	… …fi0… …
Yr	fri	fr2	…fir…	frc	…fr0…
	f01	f02	…f0j…	f0c	f00

x_i – значение признака;

c = column – столбец;

r = row – строка.

В общем виде для любого значения i = j = число объектов удовлетворяет условиям i-той строки и j-того столбца равно f_ij.

Каждая внутренняя ячейка таблицы сопряженности может содержать 4 частоты:

1) абсолютная – число объектов, удовлетворяющих условию i-той строки j-того столбца f_ij;

2) относительная – удовлетворяющая условию строки * 100% ;

3) относительная – удовлетворяющая условию столбца 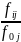* 100%;

4) относительная – рассчитанная от объёма выборочной совокупности (дающая 100% по строке – относительная частота по строке) * 100%.

Замечание: при построении таблицы сопряженности рекомендуется переменную, имеющую малое значение признака, располагать по столбцам, а переменную, имеющую большее число значений, располагать по строкам.

Используя относительные частоты, мы можем ответить на вопрос, как один признак распределяется относительно другого. Используя абсолютные частоты, мы можем ответить на вопрос, существует ли статистическая связь между двумя изучаемыми признаками. Наличие связи мы проверяем с помощью статистических гипотез. Как правило, в таблице сопряженности один признак является группирующим, а второй является смысловым. В зависимости от того, по строке или по столбцу располагается группирующий признак, мы используем относительные частоты, удовлетворяющие условиям строки или столбца.

Проверка гипотезы о наличии связи в таблице сопряженности

Для того чтобы определить наличие статистической связи между двумя качественными переменными, необходимо проверить статистическую гипотезу. Перед формулировкой гипотезы нужно построить наряду с эмпирической таблицей сопряженности теоретическую таблицу сопряженности. Теоретическая таблица сопряженности – такая таблица, в которой полностью отсутствует статистическая связь. Частота во внутренних клетках в теоретических таблицах сопряженности обозначается e_ij = .

Н₀ говорит о том, что связь таблицы сопряженности отсутствует, Н₁ – связь присутствует.

Н₀: fij = eij для всех i =

j =

H₁: fij ≠ eij для всех i =

j =

Формула критерия х² проверки гипотезы о наличии связи таблицы сопряженности:

.

В основе построения статистического критерия лежит теоретическое распределение х²:

х²_кр = х²_{1 – α;df} df = (r – 1)(c – 1)

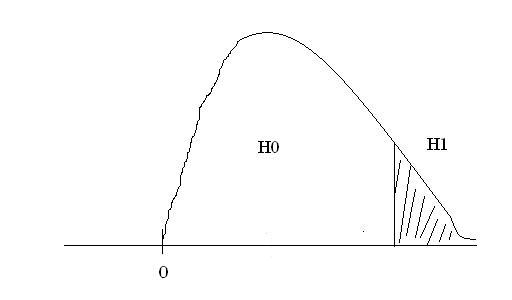
При проверке гипотезы изначально α берут равным 0,01.

Если на это уровне значимости подтверждается Н₁, проверку останавливаем: это искомый результат. Если на уровне значимости подтверждается Н₀, α меняют на равное 0,05. (Есть окончательный вывод о таблице сопряженности).

Меры (коэффициенты) связи для таблицы сопряженности

Определив наличие связи в таблице сопряженности, необходимо также рассчитать формальные показатели этой связи. В роли таких показателей выступают коэффициенты (меры связи). Все коэффициенты связи для таблицы сопряженности рассчитываются на основе статистики, вычисленной по формуле критерия:

1) коэффициент Пирсона (контингенции):

Свойства:

- если значение стремится к 0, то между изучаемыми признаками связь отсутствует;

- если значение равно 1, то между изучаемыми признаками присутствует полная статистическая связь;

2) коэффициент Чупрова для квадратных таблиц сопряженности:

Свойства:

- если значение стремится к 0, то между изучаемыми признаками связь отсутствует;

- если значение равно 1, то между изучаемыми признаками присутствует полная статистическая связь;

- промежуточные значения не интерпретируются;

3) коэффициент Крамера:

Свойства:

- если значение стремится к 0, то между изучаемыми признаками связь отсутствует;

- если значение равно 1, то между изучаемыми признаками присутствует полная статистическая связь;

- промежуточные значения не интерпретируются.