
- •1.Понятие аэромеханики. Внешняя и внутренняя задачи механики жидкости и газа. Гипотеза сплошности. Принцип обращения движения
- •2.Аэродинамическое подобие. Критерии Маха, Рейнольдца, Фруда
- •5.Силы, действующие в жидкости, нормальные и касательные напряжения. Давление, плотность и вязкость жидкости.
- •6. Кинематика. Методы Лагранжа и Эйлера описания движения жидкой частицы. Линия тока, трубка тока, струйка, их свойства.
- •7.Угловые скорости вращения жидкой частицы. Вихревая линия, трубка, шнур.
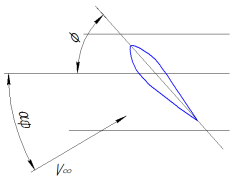
- •21. Влияние геометрических параметров профиля на его аэродинамические характеристики.
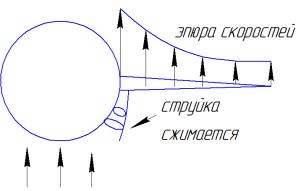
- •22. Способы увеличения максимальной подъемной силы крыла. Механизация крыла. Пограничный слой. Управление пограничным слоем, отсос и сдув пограничного слоя, реактивный закрылок.
- •31. Крылья малых удлинений.
- •32. Обтекание крыла конечного размаха сверхзвуковым потоком. Дозвуковая, сверхзвуковая передняя кромка.
- •40.Влияние интерференции на подъемную силу.
- •41. Аэродинамика высоких скоростей. Основа термодинамики. Энтальпия. Изоэнтропический процесс.
- •Вопрос 42 Параметры заторможенного потока. Критические параметры
- •51.Связь между углом поворота и углом наклона скачка.
- •52. Изменение давления при отклонения потока на малые углы.
- •53. Тонкая пластина в сверхзвуковом потоке.
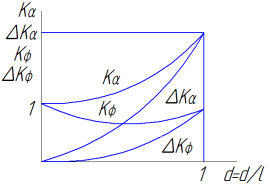
40.Влияние интерференции на подъемную силу.
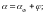 Если
имеем только
Если
имеем только
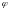 ,
то
,
то
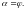 Принято учитывать влияние интерференции
на подъёмную силу при расчёте подъёмной
силы крыла.
Принято учитывать влияние интерференции
на подъёмную силу при расчёте подъёмной
силы крыла.
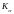 - коэффициент интерференции, учитывающий
увеличение подъёмной силы крыла при
изменении угла атаки.
- коэффициент интерференции, учитывающий
увеличение подъёмной силы крыла при
изменении угла атаки.
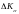 -
коэффициент интерференции, учитывающий
изменение подъёмной силы крыла от
действия Фюзеляжа при изменении угла
атаки.
-
коэффициент интерференции, учитывающий
изменение подъёмной силы крыла от
действия Фюзеляжа при изменении угла
атаки.
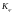 - коэффициент интерференции, учитывающий
изменение подъёмной силы крыла при
изменении угла
.
- коэффициент интерференции, учитывающий
изменение подъёмной силы крыла при
изменении угла
.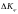 - увеличение подъёмной силы фюзеляжа
от действия крыла при изменении
.
- увеличение подъёмной силы фюзеляжа
от действия крыла при изменении
.
41. Аэродинамика высоких скоростей. Основа термодинамики. Энтальпия. Изоэнтропический процесс.
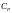 удельная теплоемкость
при Р=const.
удельная теплоемкость
при Р=const.
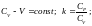
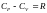 удельная газовая
постоянная.
удельная газовая
постоянная.
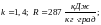 для воздуха
для воздуха
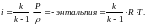
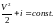
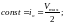
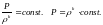

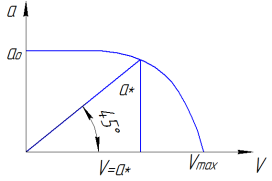
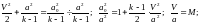
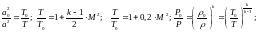
Вопрос 42 Параметры заторможенного потока. Критические параметры
Косой скачок:
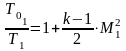
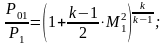
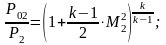
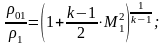
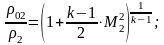
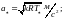
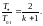
Прямой скачок:
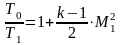
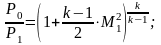
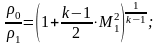
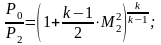
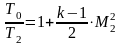
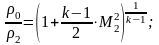
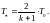
Вопрос№43. Зависимость газодинамических параметров от числа маха
Имеем уравнение энергии, в случае изоэнтропического течения, совпадающего с уравненим бернулли
Разделим
обе части на
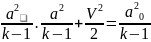
Получим
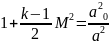
И
с учётом того, что
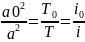 получим
получим
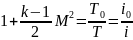
Используя
уравнение изоэнтропы и состояния получим
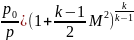 .
.
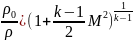
44. Приведенная скорость. Коэффициент скорости.
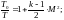
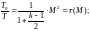 Газодинамическая
функция
Газодинамическая
функция
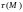
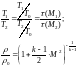 Газодинамическая
функция
Газодинамическая
функция
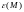
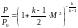 Газодинамическая
функция
Газодинамическая
функция
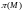
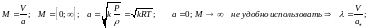
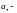 Критическая
скорость звука.
Критическая
скорость звука.
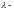 Коэффициент
скорости.
Коэффициент
скорости.
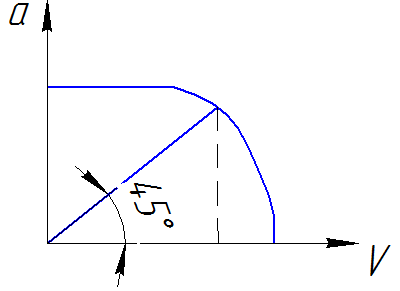
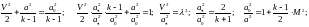
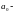 скорость
заторможенного потока.
скорость
заторможенного потока.
Получим
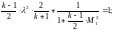
Приведем к общему знаменателю:
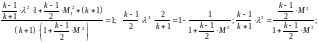
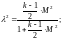 Если
Если
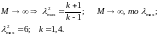
45. Зависимость между формой и скоростью струйки.
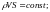 Уравнение
Неразрывности
Уравнение
Неразрывности
Дифференцируем
это выражение: разделим на
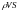
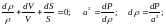
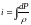 Энтальпия.
Энтальпия.
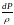 Можно представить в виде.
Можно представить в виде.
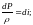
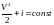 Уравнение
энергии.
Уравнение
энергии.
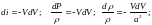
Подставим
это выражение в исходное соотношение
и перепишем в виде
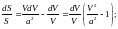
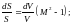 Уравнение
Гюгонио.
Уравнение
Гюгонио.
Из
уравнения следует, если
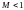 ,
то
,
то
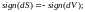
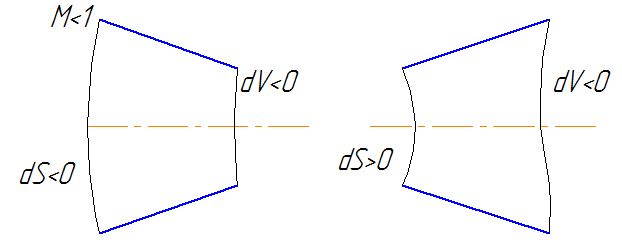
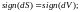
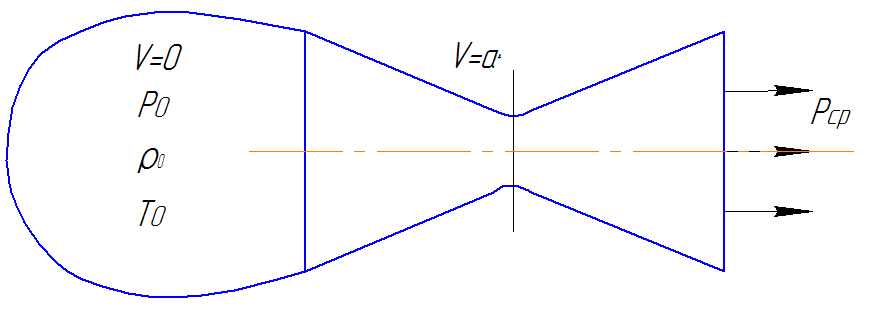
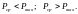
46. Теория прямого скачка уплотнения.
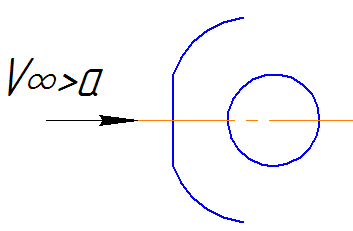
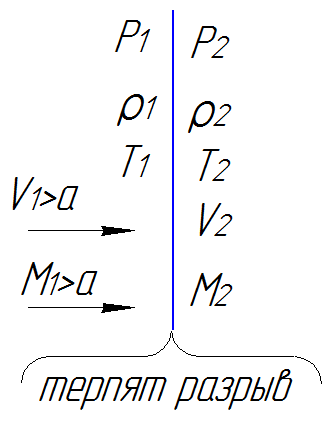
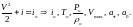
Запишем фундаментальные уравнения:
Уравнение
энергии:
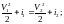
Уравнение
импульса:
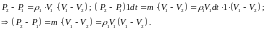
Уравнение
неразрывности:
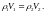
Уравнение
состояния:
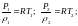
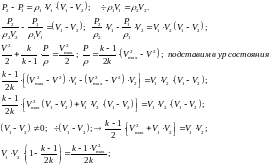
Ф.
Прандля для прямого скачка. Из формулы
следует, если
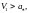 то после скачка
то после скачка
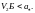
47. Изменение газодинамических параметров на прямом скачке.
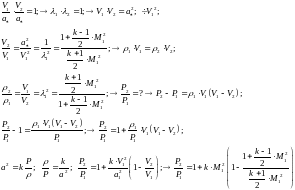
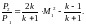
48. Связь числа Маха после скачка с числом Маха перед скачком.
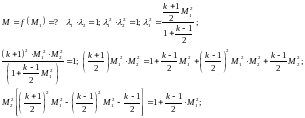
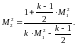
49. Давление торможения за прямым скачком уплотнения.
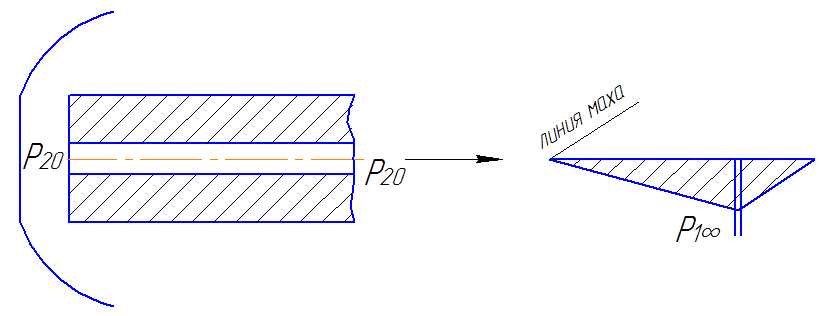
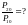
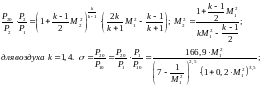
50.Косой скачок уплотнения.
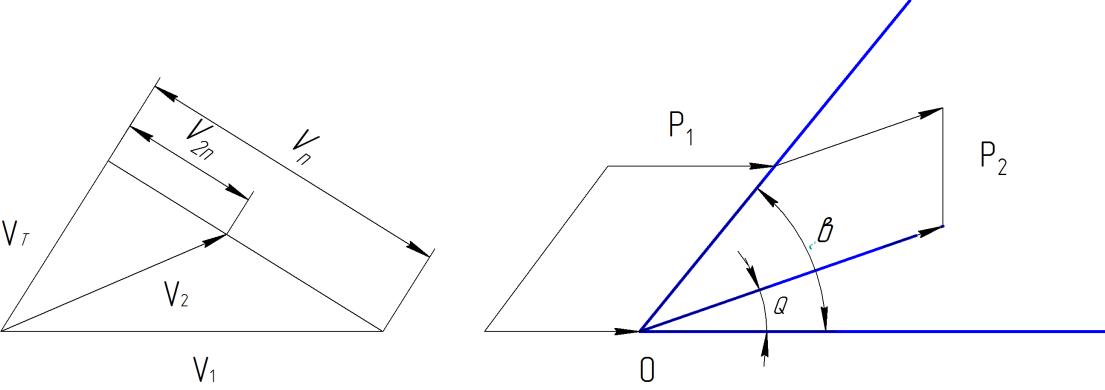
Уравнение
энергии:
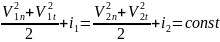 ;
;
Импульса: скачку.
Импульс= изм. кол-ва движения
скачку.
Импульс= изм. кол-ва движения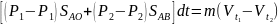 .
.
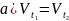 ! –тангенциальная
состовл. Скорости не терпит разрыв.
! –тангенциальная
состовл. Скорости не терпит разрыв.
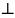 скачку.
скачку.
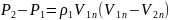
3)уравнение
неразрывности.
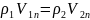 ;
;
4)уравнение
состояния
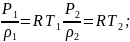 Из (а)
Из (а)
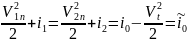
Сравнения с соотношениями для прямого скачка видим, что они одинаковы,
но
надо заметить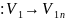 ;
;
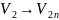 ;
;
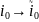 .
.
Получим
: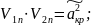
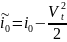 ;
;
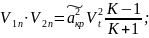
Нормальная составляющая скорости терпит разрыв на косом скачке.
После
скачка нормальная составляющая V всегда
дозвуковая:
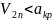 .
Т.к.
.
Т.к.
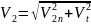
Полная
скорость после скачка может быть как
дозвуковой так и сверхзвуковой.Изменение
праметров газа на косом скачке уплотнения
будет описываться теми же уравунениями
что и при прямом скачке.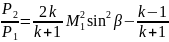 ;
;
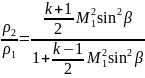 ;
так находим
;
так находим
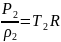 из уравнения сост.
из уравнения сост.
