Оглавление
Лекция №0 [03.09.2012] Метрология 2
Лекция №1 [10.09.2012] 3
Лекция №2 [17.09.2012] 6
Лекция №3 [24.09.2012] 9
Лекция №4 [01.10.2012] 12
Лекция №5 [08.10.2012] 14
Лекция №6 [15.10.2012] 17
Лекция №7 [22.10.2012] 20
Лекция №8 [29.10.2012] 22
Лекция №9 [05.10.2012] 23
Лекция №10 [12.11.2012] Стандартизация 26
Лекция №11 [19.11.2012] 28
Лекция №12 [26.11.2012] 30
Лекция №13 [03.11.2012] Сертификация 32
Лекция №14 [09.12.2012] 35
Лекция №15 [17.12.2012] 36
Лекция №0 [03.09.2012] Метрология Лекция №1 [10.09.2012]
Значение физической величины – выражение размера физической величины в виде некоторого числа принятых для нее единиц, (пример: при массе тела 10 кг значения величины будут соответствовать 10 кг [10 единиц массы килограммов]).
Размер физической величины – количественная определенность, присущая конкретному материальному объекту \ явлению \ процессу.
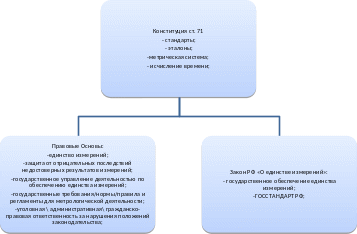
Метрологическая служба – совокупность субъектов деятельности и видов работ, направленных на обеспечение единства измерений (сеть организаций, отдельных подразделений, на которые возложена ответственность за обеспечение единства измерений).
Качественная характеристика измеряемых величин производится с помощью их размерности, обозначаемой dim. Размерность основных физических величин – длины, массы. Времени обозначается соответствующими заглавными буквами: dim l – L, dim m – M, dim t – T.
При определении размерности производных величин руководствуются следующими правилами:
1) размерности левой и правой частей уравнения должны совпадать , так как сравниваться между собой могут только одинаковые свойства. Если размерность правой и левой части уравнения не совпадают то в формуле, в какой бы области знаний она не лежала, следует искать ошибку. Объединяя левую и правую части уравнения следует помнить, что алгебраически суммироваться только величины имеющие одинаковые размерности.
2) алгебра размерностей мультипликативна, то есть состоит из одного единственного действия – умножения.
Пример:
Если Q = ABC то dim (ABC) = dim A * dim B * dim С Q – значение физической величины.
Если Q = A/B то dim Q = dim A / dim B или Q = dim A * dim B-1
Если Q = An то dim n A
Если скорость определяется как v = l/t то dim (v) = dim (l) / dim (t) = L / T = L * T-1
Если сила по второму закону ньютона равна F = ma, где a = v / t, то dim (F) = dim (m) * dim (a) =
= (M * L) / T = M * L * T-1
Размерность – это выражение отражающее связь данной величины с основными величинами системы, в котором коэффициент пропорциональности принят равным единице. Выражение представляется в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях.
Основное уравнение измерений
При измерении некоторой физической величины Q в выбранных единицах измерениях U получим результат измерения в виде формулы:
Q = nU
Q – значение физической величины
n – число единиц
U – единица физической величины
Уравнение называется основным уравнение измерений, и показывает что числовое значение величины зависит от размеров принятой единицы измерения.
Пример:
Q = n1U1 Q = n2U2
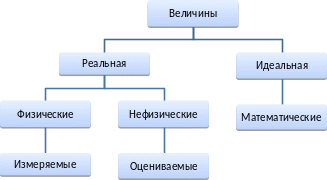
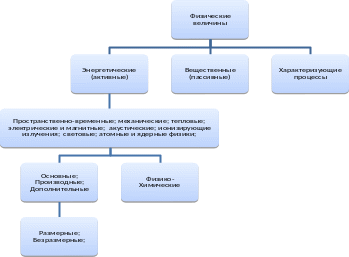
Классификация физических величин
Величина – это свойство чего-либо, которое может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно.
Свойство – это философская категория, выражающая такую сторону объекта (явления, процесса) которое обуславливает его различие и общность с другими объектами (явлениями \ процессами) и обнаруживается в его отношениях к ним.
Математическая модель объекта измерения – это совокупность математических символов (образов) и отношений между ними, которая адекватно описывает интересующие субъекта свойства объекта измерения.
Объект измерения – это реальный физический объект свойства которого характеризуются одной или несколькими измеряемыми физическими величинами.
Субъект измерения – человек, принципиально не в состоянии представить себе объект целиком, во всем многообразии его свойств и связей, вследствие этого взаимодействие субъекта с объектом возможно только на основе математической модели объекта.