Решение задач однофакторного дисперсионного анализа Пример

Три группы продавцов продавали штучный товар, расфасованный в различные упаковки. После окончания срока распродажи был произведен тестовый контроль над случайно отобранными продавцами из каждой группы. Были получены следующие результаты:

Номер группы	Число продаж, которые сделали продавцы,	Общее количество продаж	Количество продавцов, nk
1	1 3 2 1 0 2 1	10	7
2	2 3 2 1 4 -  -	12	5
3	4 5 3 -  - -  -	12	3

Если число выборок m=3, число продаж во всех выборках n=15, то:

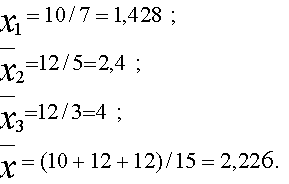
Если

,

,

тогда

Q=104–15·2,226 ²=26,93 ,

Q₁=91,074–15·2,226 ²=14,01,

Q₂=Q–Q₁=26,93–14,01=12,92.

Вычислим критерий Фишера

Сравнивая это значение с табличным F > F_0,05;2;12 =3,885, делаем вывод, что упаковка влияет на количество распродаж.

Вывод

В результате проделанной работы я выяснила следующее.

Дисперсионный анализ (анализ отклонений) - анализ и исследования причин отклонений фактических затрат от нормативных.

Анализ производится следующим образом:

5. Группируют совокупность наблюдений по факторному признаку

6. Находят среднее значение результата и дисперсию по каждой группе.

7. Определяют общую дисперсию и вычисляют, какая доля ее зависит от условий, общих для всех групп, какая — от исследуемого фактора, а какая — от случайных причин.

8. С помощью специального критерия определяют, насколько существенны различия между группами наблюдений и, следовательно, можно ли считать ощутимым влияние тех или иных факторов.

Существует две модели дисперсионного анализа:

• с фиксированными уровнями факторов,

• со случайными факторами.

В зависимости от количества факторов, определяющих вариацию результативного признака, дисперсионный анализ подразделяют на однофакторный и многофакторный.

Основными схемами организации исходных данных с двумя и более факторами являются:

• перекрестная классификация, которая характерная для моделей с фиксированными уровнями факторов

• иерархическая (гнездовая) классификация, характерная для моделей со случайными факторами.

В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе.

Однофакторный дисперсионный анализ используется для сравнения средних значений для трех и более выборок.

Недостаток: невозможно выделить те выборки, которые отличаются от других. Для этой цели необходимо использовать метод Шеффе или проводить парные сравнения выборок.

Многофакторный дисперсионный анализ, помимо функций однофакторного дисперсионного анализа, оценивает межфакторное взаимодействие.

Список используемой литературы

1. Орлов А.И. «Математика случая: Вероятность и статистика – основные факты» Учебное пособие. – М.: МЗ-Пресс, 2004. – 110 с.

2. Ветров А.А., Ломовацкий Г.И. – «Дисперсионный анализ в экономике» 1975. 120 с

3. Шеффе Г. «Дисперсионный анализ» - М.: Наука, 1980. -512 c.

4. http://bono-esse.ru/blizzard/Medstat/Statan/stat_da.html

5. http://dic.academic.ru