Практическая часть Решение задач двухфакторного дисперсионного анализ без повторений

Microsoft Excel располагает функцией: Двухфакторный дисперсионный анализ без повторений, которая используется для выявления факта влияния контролируемых факторов А и В на результативный признак на основе выборочных данных, причем каждому уровню факторов А и В соответствует только одна выборка. Для вызова этой функции необходимо на панели меню выбрать команду Сервис – Анализ данных. На экране раскроется окно Анализ данных, в котором следует выбрать значение Двухфакторный дисперсионный анализ без повторений и щелкнуть на кнопке ОК. В результате на экране раскроется диалоговое окно, показанное на рисунке 1.

Рис. 1: диалоговое окно функции

В диалоговом окне задаются следующие параметры.

1. В поле Входной материал вводится ссылка на диапазон ячеек, содержащий анализируемые данные.

2. Флажок опции Метки устанавливается в том случае, если первая строка во входном диапазоне содержит заголовки столбцов. Если заголовки отсутствуют, флажок следует сбросить. В этом случае для данных выходного диапазона будут автоматически созданы стандартные названия.

3. В поле Альфа вводится принятый уровень значимости α, соответствующий вероятности возникновения ошибки первого рода.

4. Переключатель в группе Параметры вывода может быть установлен в одно из трех положений: Выходной интервал, Новый рабочий лист или Новая рабочая книга.

Пример

Рассмотрим использование функции Двухфакторный дисперсионный анализ без повторений на следующем примере.

На рисунке. 2 представлены данные об урожайности (ц/га) четырех сортов пшеницы (четыре уровня фактора А), достигнутой при использовании пяти типов удобрений (пять уровней фактора В). Данные получены на 20 участках одинакового размера и аналогичного почвенного покрова. Необходимо определить, влияет ли сорт и тип удобрения на урожайность пшеницы.

Рис. 2: данные об урожайности

Результаты двухфакторного дисперсионного анализа с помощью функции Двухфакторный дисперсионный анализ без повторений представлены на рисунке 3.

Как видно по результатам, расчетное значение величины F-статистики для фактора А (тип удобрения) F^А=l,67, а критическая область образуется правосторонним интервалом (3,49; +∞). Так как F^А=l,67 не попадает в критическую область, гипотезу Н_А: a₁ = a₂ + … = a_k принимаем, т.е. считаем, что в этом эксперименте тип удобрения не оказал влияния на урожайность.

Р ис. 3: Результаты двухфакторного дисперсионного анализа

Расчетное значение величины F-статистики для фактора В (сорт пшеницы) F^В =2,03, а критическая область образуется правосторонним интервалом (3,259;+∞).

Так как F^В =2,03 не попадает в критическую область, гипотезу Н_В: b₁ = b₂ = ... = b_m

также принимаем, т.е. считаем, что в данном эксперименте сорт пшеницы также не оказал влияния на урожайность.

Решение задач двухфакторного дисперсионного анализа c повторениями

Microsoft Excel располагает функцией: Двухфакторный дисперсионный анализ с повторениями, которая также используется для выявления факта влияния контролируемых факторов А и В на результативный признак на основе выборочных данных, однако каждому уровню одного из факторов А (или В) соответствует более одной выборки данных.

Рассмотрим использование функции Двухфакторный дисперсионный анализ с повторениями на следующем примере.

Пример

В таблице. 3 приведены суточные привесы (г) собранных для исследования 18 поросят в зависимости от метода удержания поросят (фактор А) и качества их кормления (фактор В).

Количество голов в группе (фактор А)	Содержание протеина в корме, г (фактор В)
	В1=80	В2=100
А1-30	530, 540, 550	600, 620, 580
А2=100	490, 510, 520	550, 540, 560
А3=300	430, 420, 450	470, 460, 430

Таблица 3: суточные привесы собранных для исследования 18 поросят

Необходимо оценить существенность (достоверность) влияния каждого фактора и их взаимодействия на суточный привес поросят.

На рисунке 4 порядок ввода данных на рабочий лист табличного процессора Microsoft Excel.

Рис. 4: Порядок ввода данных

Для вызова необходимой функции необходимо на панели меню выбрать команду Сервис – Анализ данных. На экране раскроется диалоговое окно Анализ данных, в котором следует выбрать значение: Двухфакторный дисперсионный анализ с повторениями и щелкнуть на кнопке ОК. В результате на экране раскроется диалоговое окно Двухфакторный дисперсионный анализ с повторениями, показанное на рисунке 5.

Р ис. 5: Диалоговое окно функции

В этом диалоговом окне задаются следующие параметры.

1. В поле Входной интервал вводится ссылка на диапазон ячеек, содержащий анализируемые данные. Необходимо выделить ячейки от G 4 до I 13.

2. В поле Число строк для выборки определяется число выборок, которое приходится на каждый уровень одного из факторов. Каждый уровень фактора должен содержать одно и то же количество выборок (строк таблицы). В нашем случае число строк равно трем.

3. В поле Альфа вводится принятое значение уровня значимости α, которое равно вероятности возникновения ошибки первого рода.

4. Переключатель в группе Параметры вывода может быть установлен в одно из трех положений: Выходной интервал, Новый рабочий лист или Новая рабочая книга.

Результаты двухфакторного дисперсионного анализа с помощью функции Двухфакторный дисперсионный анализ с повторениями представлены на рисунке 6.

Р ис. 6: Результаты двухфакторного дисперсионного анализа

Очевидно, данные факторы имеют фиксированные уровни, т.е. мы находимся в рамках модели I. Поэтому для проверки существенности влияния факторов А, В и их взаимодействия АВ необходимо найти отношения

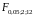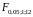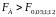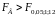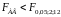и сравнить их с табличными значениями соответственно :=3,88; =: =4,75; =3,88. Так как и то влияние метода содержания поросят (фактора А) и качества их кормления (фактора В) является существенным. В силу того что взаимодействие указанных факторов незначимо (на 5%-ном уровне).