
- •Введение
- •Теоретическая часть Основные понятия
- •Однофакторный дисперсионный анализ
- •Двухфакторная модель
- •Многофакторный дисперсионный анализ
- •Практическая часть Решение задач двухфакторного дисперсионного анализ без повторений
- •Решение задач двухфакторного дисперсионного анализа c повторениями
- •Решение задач однофакторного дисперсионного анализа Пример
- •Список используемой литературы
Однофакторный дисперсионный анализ
Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак.
Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении более двух независимых выборок, полученных из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.
Для этих выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли этот фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).
Пусть
![]() – i – элемент (
– i – элемент (![]() )
)
![]() - выборки (
- выборки (![]() ),
где m – число выборок, nk – число данных
в
-
выборке. Тогда
),
где m – число выборок, nk – число данных
в
-
выборке. Тогда
![]() – выборочное среднее
-выборки
определяется по формуле
– выборочное среднее
-выборки
определяется по формуле
 .
.
Общее среднее вычисляется по формуле
 ,
где
,
где

Основное тождество дисперсионного анализа имеет следующий вид:
![]() ,
,
Где
Q1 – сумма квадратов отклонений выборочных
средних
![]() от общего среднего
от общего среднего
![]() (сумма квадратов отклонений между
группами);
(сумма квадратов отклонений между
группами);
Q2 –
сумма квадратов отклонений наблюдаемых
значений
![]() от выборочной средней
(сумма квадратов отклонений внутри
групп); Q – общая сумма квадратов
отклонений наблюдаемых значений
от общего среднего
от выборочной средней
(сумма квадратов отклонений внутри
групп); Q – общая сумма квадратов
отклонений наблюдаемых значений
от общего среднего
![]() .
.
Расчет этих сумм квадратов отклонений осуществляется по следующим формулам:
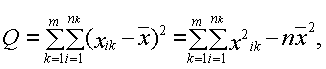
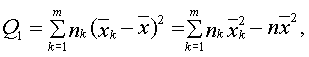

В качестве критерия необходимо воспользоваться критерием Фишера:
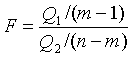 .
.
Если
расчетное значение критерия Фишера
будет меньше, чем табличное значение
![]() – нет оснований считать, что независимый
фактор оказывает влияние на разброс
средних значений, в противном случае,
независимый фактор оказывает существенное
влияние на разброс средних значений
(λ– уровень значимости, уровень риска,
обычно для экономических задач λ=0,05).
– нет оснований считать, что независимый
фактор оказывает влияние на разброс
средних значений, в противном случае,
независимый фактор оказывает существенное
влияние на разброс средних значений
(λ– уровень значимости, уровень риска,
обычно для экономических задач λ=0,05).
Недостаток однофакторного анализа: невозможно выделить те выборки, которые отличаются от других. Для этой цели необходимо использовать метод Шеффе или проводить парные сравнения выборок.
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Средний квадрат |
Математическое ожидание среднего квадрата |
Межгрупповая |
|
m-1 |
|
|
Внутригрупповая |
|
mn-m |
= Q2/(mn-m)
|
M(S |
Общая |
|
mn-1 |
|
|
Таблица 1: Базовая таблица однофакторного дисперсионного анализа
В таблице представлен общий вид вычисления значений, с помощью дисперсионного анализа.
Двухфакторная модель
Одной из используемых моделей данных в дисперсионном анализе является двухфакторная модель. Она состоит в учёте систематических (первый фактор) и случайных (второй фактор) ошибок в определении измеряемых параметров.
Пусть
с помощью методов
![]() производится измерение нескольких
параметров, чьи точные значения —
производится измерение нескольких
параметров, чьи точные значения —
![]() .
В таком случае, результаты измерений
различных величин различными методами
можно представить как:
.
В таком случае, результаты измерений
различных величин различными методами
можно представить как:
![]() ,
,
где:
![]() — результат измерения
— результат измерения
![]() -го
параметра по методу
-го
параметра по методу
![]() ;
;
![]() — точное значение
-го
параметра;
— точное значение
-го
параметра;
![]() —
систематическая ошибка измерения
-го
параметра по методу
;
—
систематическая ошибка измерения
-го
параметра по методу
;
![]() —
случайная ошибка измерения
-го
параметра по методу
.
—
случайная ошибка измерения
-го
параметра по методу
.
Тогда
дисперсии случайных величин
,
![]() ,
,
![]() ,
,
![]() , где:
, где:
![]()


выражаются как:


![]()

и удовлетворяют тождеству:
![]()
Двухфакторная схема позволяет лишь обнаружить систематические расхождения, но непригодна для их численной оценки с последующим исключением из результатов наблюдений. Эта цель может быть достигнута только при многократных измерениях (то есть при повторных использованиях указанной схемы над данными повторных экспериментов).

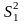 =
Q1/(m-1)
=
Q1/(m-1)

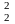 )=
σ2
)=
σ2