Граничные условия для векторов магнитного поля
тангенциальные составляющие
Три взаимно ортогональных единичных вектора lτ,ln,lk введем в точке P. Е диничными векторами нормального и тангенциального направлений по-прежнему являются два из них, а вектор lk создаст нормаль к плоскости, образованной двумя первыми векторами и лежит в плоскости границы раздела. В окрестности точки Р со сторонами ∆l и ∆h (∆h<<∆l)
выделим достаточно малый прямоугольный контур лежащий в плоскости, образованной векторами lτ и ln. Будем полагать, что задано такое направление обхода на контуре, которое наблюдается с конца вектора lk против часовой стрелки. К контуру используем закон полного тока, будем полагать, что достаточно малы размеры сторон контура для того, чтобы считать в их пределах векторы поля Н постоянными. В итоге получим:
Н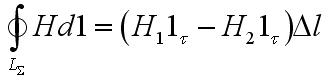
а
данном этапе нужно разобрать два случая:
1. Величинами конечными являются электродинамические параметры обеих граничащих сред. Здесь же непосредственно вытекает конечное значение векторов плотности токов проводимости и смещения. Произведем предельный переход, направляя высоту контура ∆h к нулю. При этом будет равна нулю также величина циркуляции вектора Н. Будем иметь:
Т
ем
самым, непрерывны тангенциальные
составляющие векторов напряженности
магнитного поля в конечных значениях
электродинамических параметров сред.
Вот тут следует, что терпят разрыв
тангенциальные составляющие векторов
магнитной индукции:
2
.
Бесконечна проводимость одной из
граничащих сред. Ток проводимости будет
протекать по тонкой пленке и lim
правой части не равен 0.
В целях характеристики токов, протекающих
по поверхности безупречного проводника,
вводят представление вектора плотности
поверхностного тока η.
Для начала, проводится касательный к линиям тока в данной точке единичный вектор, который обозначается через ln. Далее находится величина тока ∆i, проходящего через отрезок ∆l, перпендикулярный вектору ln. Затем определяется плотность поверхностного тока как
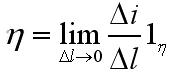
С
ледом
необходимо учесть, что внутри безупречного
проводника должны равняться нулю все
составляющие электромагнитного поля.
Отчего H2=0,
получим
H1lτ=ηlk
С тем учетом, что
lτ=-[ln lk]
можно записать
η=[ln H1]
Тем самым, на границе раздела с идеальным металлом поверхностный ток протекает в направлении, перпендикулярном вектору H1, а также численно равен напряженности магнитного поля.
Векторный и скалярный потенциалы эл/м поля
Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. А соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля. Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:
С
уществует
следующее векторное тождество:
B=rot A
(5)
Векторную функцию A называют векторным электрическимпотенциалом. Соотношение (5) при известном A однозначно определяет вектор H. Обратное определение неоднозначно, т.е. при известном векторном поле H соотношение (5) определяет A неоднозначно. Известно, что rot grad =0. Поэтому, если ввести A и A=A+frad U, то соотношение (5) не изменится. Поэтому соотношение (5) определяет A с точностью до градиента произвольной функции.
Скалярную функцию U называют скалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал.