Плоские эл/м волны.

Проанализируем бескрайнее трехмерное пространство с декартовой системой координат х, у, z. У которого в каждой точке задана некоторая величина А (её физическая природа безразлична), меняющаяся в пространстве и во времени по закону

В пространстве (в предоставленном моменте) имеется монохроматическая плоская волна. Называемый фазой волны ωt-+βz – аргумент косинуса является пространственной координаты z и функцией времени t. Если же z зафиксировать, то величина А приобретает такие же значения через небольшие промежутки времени, кратные периоду T=2π/ω. Если зафиксировано время, то величина А периодически изменяется вдоль оси z с периодом λ именуемым длиной волны. Величины β и λ связаны между собой:

β=2π/λ

Число β служит значимой характеристикой волнового процесса и называется постоянной распространения волны. Также могут использоваться термины как волновое число и фазовая постоянная. Весь смысл величины β с физической стороны в том, что она указывает, на сколько радиан фаза волны изменяется в прохождении одного метра пути. Нахождение двух потенциальных знаков в формуле

с огласованно с тем, что плоские волны вполне могут исходить в двух противоположных направлениях.

Именуем поверхность, волновым фронтом плоской волны, удовлетворяющую уравнению

ωt-+βz =const

Вполне понятно, что в данном случае волновые фронты представляют собой бесконечные плоскости, перемещающиеся в пространстве со скоростью

н осящей название фазовой скорости и перпендикулярные оси z. От того, что время изменяется постоянно лишь в одном направлении, уравнение

ωt-βz =const

отвечает фронту волны, источающейся в направлении положительной оси z. К изменению направления её распространения ведет изменение знака в фазе волны. Подключим комплексные амплитуды плоских волн.

о пределённо для волны, подходящей в противоположную сторону

В любой реальной среде распространение волн неминуемо за счёт тепловых потерь сопровождается понижением их амплитуды. Закон затухания:

Т ут α несёт название постоянной затухания волны. Введя комплексную постоянную распространения γ можно объединить величины β и α, то есть

γ=β -iα

Таким образом, вещественная часть γ находит закон изменения фазы в распространяющейся волне, в тот момент как мнимая часть характеризует затухание.

Сферические волны

Такой волновой тип получается в случаях, когда точечный источник возбуждает однородное неограниченное пространство. Простейший случай, в котором только от радиальной координаты r зависит амплитуда колебания:

и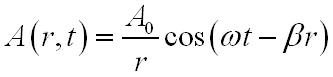 ли же, если сформулировать величину A (r,t) через её комплексную амплитуду

Ц илиндрические волны

Источник — бесконечные нити. При этом волновые фронты обладают видом концентрических цилиндров. На расстоянии от оси значительно превышающем длину волны справедливо следующее приближенное равенство:

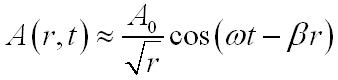
Однородная плоская эл/м волна с линейной поляризацией

Относительно рассматриваемой плоской волны приведём следующие предположения:

а ) ориентирован вдоль оси z комплексный вектор Пойнтинга причем единственная составляющая вещественна:

о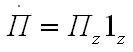 ткуда следует, что продольные составляющие магнитного и электрического полей в рассматриваемой плоской волне равны нулю:

E_z=0 H_z=0

б) плоская волна однородна, то есть вдоль волнового фронта амплитуды полей неизменны; от того, что все волновые фронты полностью параллельны плоскости XOY, крайнее условие записывается математически следующим образом:

в ) из возможных двух поперечных составляющих электрического вектора E`<sub>x</sub> и E`_y лишь E`_x отлична от нуля. Тем самым, в плоскости XOY колеблется электрический вектор. Плоскость эта именована плоскостью поляризации, а сама волна – плоской волной с линейной поляризацией. Система уравнений Гельмгольца

с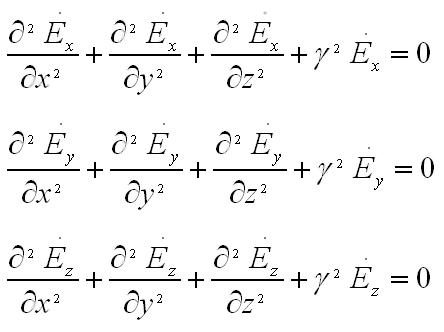 учетом сделанных предположений, сравнительно составляющих электрического вектора обращается в единственное уравнение

З нак частной производной в этом уравнении сменен на знак обыкновенной производной, потому что неизвестная функция зависит лишь от координаты z. Решение представленного уравнения в общем положении имеет следующий вид:

Г де A`<sub>1</sub> и A`₂, - произвольные, вообще говоря, комплексные, постоянные. Положим для определенности A`₂=0 , тогда

О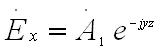 пределим магнитный вектор в данной плоской волне

о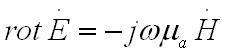 ткуда следует

Р аскрыв операцию rot, убеждаемся, что

В итоге, вектор магнитного поля представленной плоской волне располагает лишь составляющей H`y, таким образом, перпендикулярен к вектору электрического поля. Крайне важно отметить, что, между составляющими как это следует из

м агнитного и электрического полей имеется пропорциональность:

В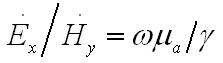 ывод отсюда состоит в следующем, при отсутствии потерь в среде, то есть при γ вещественном, поля E` и H` колеблются в фазе. Это означает, в соответствии с

ч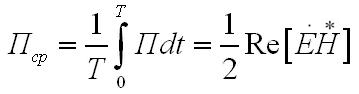 то плоская электромагнитная волна в среде переносит без потерь только активную мощность.

Zc - некоторая постоянная, которая имеет размерность сопротивления и называется характеристическим (волновым) сопротивлением данной среды.