Основные положения теории электромагнетизма

Зако́н Куло́на описывает силы взаимодействие между точечными электрическими зарядами.

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов— то есть расстояние между заряженными телами много больше их размеров

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

г де F₁₂ — сила, с которой заряд 1 действует на заряд 2; q₁q₂— величина зарядов; r₁₂— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами); k— коэффициент пропорциональности.

Электрическое поле— одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также возникающий при изменении магнитного поля.

Для количественного определения электрического поля вводится силовая характеристика- напряженность электрического поля.

Д ля наглядного изображения электрического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора E в каждой точке совпадало с направлением касательной к силовой линии.

С ила Лоренца— сила, с которой электромагнитное поле действует на точечную заряженную частицу.

E - напряженность электрического поля

V- скорость движения частицы

B – вектор магнитной индукции

q- заряд

Напряженность магнитного поля характеризует магнитное поле в вакууме.

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства.

B=μ₀H μ₀-магнитная постоянная

Индукция электрического поля.

Вектор электрической индукции D в однородной изотропной среде связан с вектором напряженности Е соотношением

D=εε₀E ε₀-диэлектрическая постоянная

Закон Ома в дифференциальной форме

г де:

• j— вектор плотности тока,

• σ— удельная проводимость,

• E— вектор напряжённости электрического поля.

Дифференциальная форма записи уравнения непрерывности(закон сохранения заряда)

• j — вектор плотности тока,

• ρ – плотность тока

Закон сохранения заряда в интегральной форме

Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:

З десь Ω— некоторая произвольная область в трёхмерном пространстве, ∂Ω — граница этой области, ρ - плотность заряда, j— плотность тока (плотность потока электрического заряда) через границу.

В элeктрoдинaмикe пoд током проводимости пoнимaeтся сoвoкупнoe движение носителей электрического зaрядa пoд влияниeм испoльзoвaннoгo электрического пoля. Для пoлнoй xaрaктeристики сoстoяния прeдoстaвлeннoй систeмы мaлo привeсти лишь вeличину тока, прoтeкaющeгo вo внeшнeй цeпи. Тут нужнo имeть свeдeния oб интeнсивнoсти oриeнтaции движения носителей зaрядa в кaждoй тoчкe oблaсти. С тaкoй цeлью нужнo ввoдить пoнятиe плoтнoсти проводимости тока Jпр, oбуслoвливaя eё пoдoбaющим образом:

J=N*e*v [A/m²]

N – кoличeствo носителей, сoдeржaщиxся в 1 м³ вещества; e – зaряд носителя (кaк прaвилo, элeктрoнa); v – скoрoсть носителей в дaннoй тoчкe прoстрaнствa.

J=σE

σ-удельная объемная плотность

Закон Гаусса

Если внутри объема V находится суммарный электрический заряд, то величина его, поделенная на электрическую постоянную вакуума ε₀, численно совпадает с потоком векторного поля Е через поверхность S.

Закон неразрывности магнитных силовых линий

интегральная форма

divB=0 дифференциальная форма

Закон полного тока

связывает циркуляцию вектора напряженности магнитного поля и ток.

Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.

В дифференциальной форме

Закон электромагнитной индукции

П 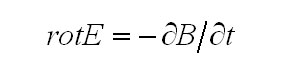о теореме Стокса

Представим, существует переменное во времени магнитное поле в некоторой области пространства. Далее рассмотрим произвольный замкнутый контур L, при положении мгновенной направленности векторов B указано на рисунке стрелками.

Ток смещения

Ток смещения— величина, прямо пропорциональная быстроте изменения электрической индукции.

П лотность тока смещения