60. Метод искусственного базиса. М-задача. Теорема о связи между решениями исходной задачи и м-задачи.

Метод искусственного базиса.

Метод искусственного базиса используется для нахождения допустимого базисного решения задачи линейного программирования, когда в условии присутствуют ограничения типа равенств. Рассмотрим задачу:

max{F(x)=∑cixi|∑ajixi=bj, j=1,m; xi≥0}.

В ограничения и в функцию цели вводят так называемые «искусственные переменные» Rj следующим образом:

∑ajix+Rj=bj, j=1,m;F(x)=∑cixi-M∑Rj

При введении искусственных переменных в методе искусственного базиса в функцию цели им приписывается достаточно большой коэффициент M, который имеет смысл штрафа за введение искусственных переменных. В случае минимизации искусственные переменные прибавляются к функции цели с коэффициентом M. Введение искусственных переменных допустимо в том случае, если в процессе решения задачи они последовательно обращаются в нуль.

Симплекс-таблица, которая составляется в процессе решения, используя метод искусственного базиса, называется расширенной. Она отличается от обычной тем, что содержит две строки для функции цели: одна – для составляющей F = ∑cixi, , а другая – для составляющей M ∑Rj Рассмотрим процедуру решения задачи на конкретном примере.

Пример 1. Найти максимум функции F(x) = -x1 + 2x2 - x3 при ограничениях:

2x1+3x2+x3=3,

x1+3x3=2,

x1≥0, x2≥0, x3≥0 .

Применим метод искусственного базиса. Введем искусственные переменные в ограничения задачи

2x1 + 3x2 + x3 + R1 = 3;

x1 + 3x3 + R2 = 2 ;

Функция цели F(x)-M ∑Rj= -x1 + 2x2 - x3 - M(R1+R2).

Выразим сумму R1 + R2 из системы ограничений: R1 + R2 = 5 - 3x1 - 3x2 - 4x3, тогда F(x) = -x1 + 2x2 - x3 - M(5 - 3x1 - 3x2 - 4x3) .

При составлении первой симплекс-таблицы (табл. 1) будем полагать, что исходные переменные x1, x2 , x3 являются небазисными, а введенные искусственные переменные – базисными. В задачах максимизации знак коэффициентов при небазисных переменных в F- и M-строках изменяется на противоположный. Знак постоянной величины в M-строке не изменяется. Оптимизация проводится сначала по M-строке. Выбор ведущих столбца и строки, все симплексные преобразования при испльзовании метода искусственного базиса осуществляются как в обычном симплекс-методе.

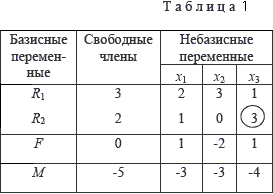
Максимальный по абсолютному значению отрицательный коэффициент (-4) определяет ведущий столбец и переменную x3, которая перейдет в базис. Минимальное симплексное отношение (2/3) соответствует второй строке таблицы, следовательно, переменная R2 должна быть из базиса исключена. Ведущий элемент обведен контуром.

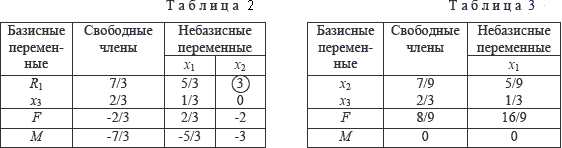
В методе искусственного базиса искусственные переменные, исключенные из базиса, в него больше не возвращаются, поэтому столбцы элементов таких переменных опускаются. Табл. 2. сократилась на 1 столбец. Осуществляя пересчет этой таблицы, переходим к табл. 3., в которой строка M обнулилась, ее можно убрать. После исключения из базиса всех искусственных переменных получаем допустимое базисное решение исходной задачи, которое в рассматриваемом примере является оптимальным:

x1=0; x2=7/9; Fmax=8/9.

Если при устранении M-строки решение не является оптимальным, то процедура оптимизации продолжается и выполняется обычным симплекс-методом. Рассмотрим пример, в котором присутствуют ограничения всех типов:≤,=,≥

М-задача

Условие задачи

Найти оптимальные величины производства продукции видов А, Б и В. Затраты сырья на единицу продукции: А – 5, Б – 2, В – 4. Объем сырья – 2000 единиц. Затраты оборудования на единицу продукции: А – 4, Б – 5, В – 4. Объем оборудования – 1000 единиц. Прибыль от реализации единицы продукции: А – 10, Б – 8, В – 12. Критерий – максимум прибыли предприятия. Производство продукции А должно быть не менее 100 ед. Производство продукции Б должно быть не менее 50 ед.

Решение задачи симплекс М методом

1) Определение оптимального плана производства

Пусть x1, x2, x3 - количество произведенной продукции вида А, Б, В, соответственно. Тогда математическая модель задачи имеет вид:

F = 10·x1 + 8·x2 + 12·x3 –>max

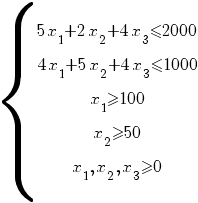
Вводим дополнительные переменные x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0, чтобы неравенства преобразовать в равенства.

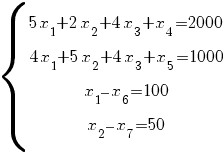
Чтобы выбрать начальный базис, вводим искусственные переменные x8 ≥ 0, x9 ≥ 0 и очень большое число M (M –> ∞). Решаем М методом.

F = 10·x1 + 8·x2 + 12·x3 + 0·x4 + 0·x5 + 0·x6 + 0·x7– M·x8– M·x9 –>max

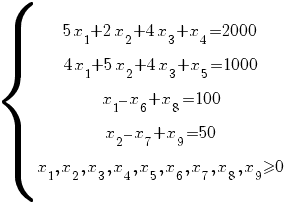
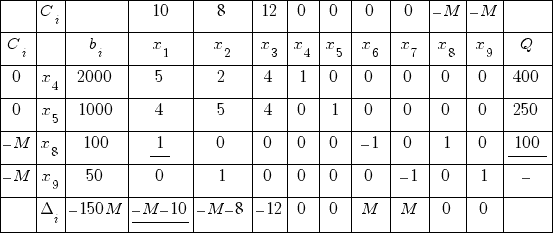
В качестве базиса возьмем x4 = 2000; x5 = 1000; x8 = 100; x9 = 50.

Данные заносим в симплекс таблицу

Симплекс таблица № 1

Ц елевая функция:

0 · 2000 + 0 · 1000 + (– M) · 100 + (– M) · 50 = – 150M

Вычисляем оценки по формуле:

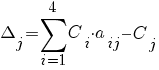
Δ1 = 0 · 5 + 0 · 4 + (– M) · 1 + (– M) · 0 – 10 = – M – 10

Δ2 = 0 · 2 + 0 · 5 + (– M) · 0 + (– M) · 1 – 8 = – M – 8

Δ3 = 0 · 4 + 0 · 4 + (– M) · 0 + (– M) · 0 – 12 = – 12

Δ4 = 0 · 1 + 0 · 0 + (– M) · 0 + (– M) · 0 – 0 = 0

Δ5 = 0 · 0 + 0 · 1 + (– M) · 0 + (– M) · 0 – 0 = 0

Δ6 = 0 · 0 + 0 · 0 + (– M) · (–1) + (– M) · 0 – 0 = M

Δ7 = 0 · 0 + 0 · 0 + (– M) · 0 + (– M) · (–1) – 0 = M

Δ8 = 0 · 0 + 0 · 0 + (– M) · 1 + (– M) · 0 – (– M) = 0

Δ9 = 0 · 0 + 0 · 0 + (– M) · 0 + (– M) · 1 – (– M) = 0

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:

Δ1 = – M – 10

Вводим переменную x1 в базис.

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение

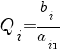для столбца x1.

Наименьшее неотрицательное: Q4 = 50. Выводим переменную x9 из базиса и удаляем искусственные переменные. Выполняем линейные преобразования.

Из 1-й строки вычитаем 4-ю строку, умноженную на 2Из 2-й строки вычитаем 4-ю строку, умноженную на 5

Получаем новую таблицу:

Симплекс таблица № 3

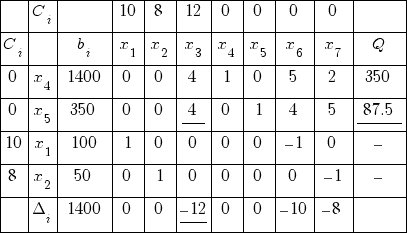
Целевая функция:

0 · 1400 + 0 · 350 + 10 · 100 + 8 · 50 = 1400

Вычисляем оценки по формуле:

Δ1 = 0 · 0 + 0 · 0 + 10 · 1 + 8 · 0 – 10 = 0

Δ2 = 0 · 0 + 0 · 0 + 10 · 0 + 8 · 1 – 8 = 0

Δ3 = 0 · 4 + 0 · 4 + 10 · 0 + 8 · 0 – 12 = – 12

Δ4 = 0 · 1 + 0 · 0 + 10 · 0 + 8 · 0 – 0 = 0

Δ5 = 0 · 0 + 0 · 1 + 10 · 0 + 8 · 0 – 0 = 0

Δ6 = 0 · 5 + 0 · 4 + 10 · (–1) + 8 · 0 – 0 = – 10

Δ7 = 0 · 2 + 0 · 5 + 10 · 0 + 8 · (–1) – 0 = – 8

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:

Δ3 = – 12

Вводим переменную x3 в базис.

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное

отношение

для столбца x3.

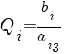
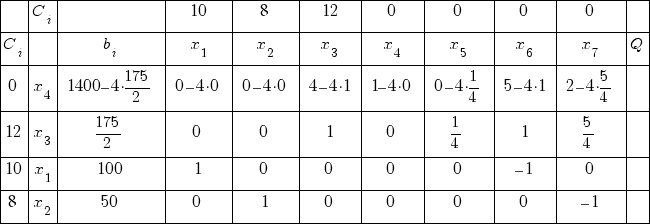
Наименьшее неотрицательное: Q2 = 87.5. Выводим переменную x5 из базиса

2-ю строку делим на 4.Из 1-й строки вычитаем 2-ю строку, умноженную на 4

Вычисляем:

Получаем новую таблицу:

Симплекс таблица № 4

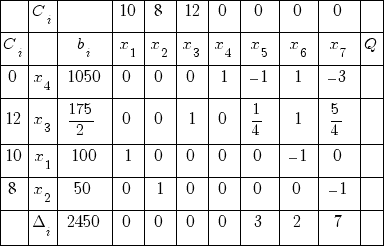
Ц елевая функция:

0 · 1050 + 12 · 175/2 + 10 · 100 + 8 · 50 = 2450

Вычисляем оценки по формуле:

Δ1 = 0 · 0 + 12 · 0 + 10 · 1 + 8 · 0 – 10 = 0

Δ2 = 0 · 0 + 12 · 0 + 10 · 0 + 8 · 1 – 8 = 0

Δ3 = 0 · 0 + 12 · 1 + 10 · 0 + 8 · 0 – 12 = 0

Δ4 = 0 · 1 + 12 · 0 + 10 · 0 + 8 · 0 – 0 = 0

Δ5 = 0 · (–1) + 12 · 1/4 + 10 · 0 + 8 · 0 – 0 = 3

Δ6 = 0 · 1 + 12 · 1 + 10 · (–1) + 8 · 0 – 0 = 2

Δ7 = 0 · (–3) + 12 · 5/4 + 10 · 0 + 8 · (–1) – 0 = 7

Поскольку отрицательных оценок нет, то план оптимален.

Решение задачи: x1 = 100; x2 = 50; x3 = 175/2 = 87.5; x4 = 1050; x5 = 0; x6 = 0; x7 = 0; Fmax = 2450

Ответ: x1 = 100; x2 = 50; x3 = 175/2 = 87.5; x4 = 1050; x5 = 0; x6 = 0; x7 = 0; Fmax = 2450То есть необходимо произвести x1 = 100 единиц продукции вида А, x2 = 50 единиц продукции вида Б и x3 = 87,5 единиц продукции вида В. Максимальная прибыль при этом составит Fmax = 2450 единиц.

Теорема о связи между решениями исходной задачи и М-задачи.

???????????????????????