Различные формы записи злп

1.Общая

2.Каноническая

3. Стандартная

54. Приведение любой ЗЛП к стандартному виду. Переход от ЗЛП в стандартном виде к ЗЛП с ограничениями-неравенствами.

?????????????????????????????????????????????????????????????????????????????????

55. Геометрическая интерпретация ЗЛП. Графический метод решения ЗЛП.

Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n =2 и n =3.

Наиболее наглядна эта интерпретация для случая n =2, т.е. для случая двух переменных и . Пусть нам задана задача линейного программирования в стандартной форме

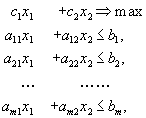
Возьмём на плоскости декартову систему координат и каждой паре чисел поставим в соответствие точку на этой плоскости.

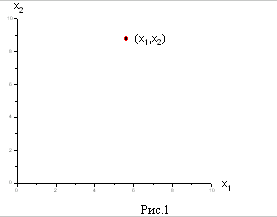
Обратим прежде всего внимание на ограничения и . Они из всей плоскости вырезают лишь её первую четверть (см. рис. 1). Рассмотрим теперь, какие области соответствуют неравенствам вида . Сначала рассмотрим область, соответствующую равенству . Как Вы, конечно, знаете, это прямая линия. Строить её проще всего по двум точкам.

Пусть . Если взять , то получится . Если взять , то получится . Таким образом, на прямой лежат две точки и . Дальше через эти две точки можно по линейке провести прямую линию

Если же b=0, то на прямой лежит точка (0,0). Чтобы найти другую точку, можно взять любое отличное от нуля значение и вычислить соответствующее ему значение .

Эта построенная прямая разбивает всю плоскость на две полуплоскости. В одной её части , а в другой наоборот . Узнать, в какой полуплоскости какой знак имеет место проще всего посмотрев, какому неравенству удовлетворяет какая-то точка плоскости, например, начало координат, т.е. точка (0,0).

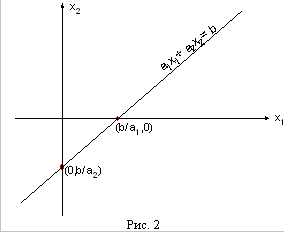
Пример

Определить полуплоскость, определяемую неравенством .

Решение

Сначала строим прямую . Полагая получим или . Полагая получим или . Таким образом, наша пря- мая проходит через точки (0, -1/2) и (3/4, 0).

Теперь посмотрим, в какой полуплоскости лежит точка (0,0), т.е. начало координат. Имеем , т.е. начало координат принадлежит полуплоскости, где . Тем самым определилась и нужная нам полуплоскость

Вернёмся теперь к задаче линейного программирования. Там имеют место m неравенств.

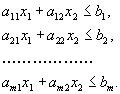
Каждое из них задает на плоскости некоторую полуплоскость. Нас интересуют те точки, которые удовлетворяют всем этим m неравенствам , т.е. точки, которые принадлежат всем этим полуплоскостям одновременно. Следовательно, область, определяемая неравенствами вида (1.20), геометрически изображается общей частью (пересечением) всех полуплоскостей, определяемых отдельными ограничениями (к ним,естественно, надо добавить ограничения и ).

Графический метод решения злп

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения.

Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования.

Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х1, х2} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c1x1 + c2x2 = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

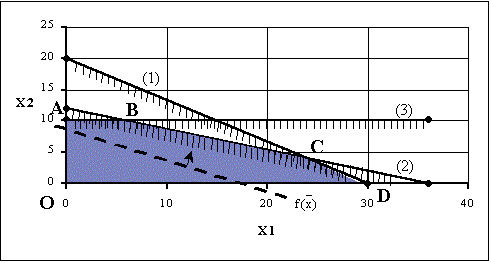
Z= 2x1 + 4x2 → max;

x1 ≥ 0, x2 ≥ 0.

2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи (см. рисунок 2.1). Эти прямые обозначены на рисунке (1), (2) и (3).

3. Штрихи на прямых указывают полуплоскости, определяемые ограничениями задачи.

4. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В нашем случае область представляет собой пятиугольник (на рисунке обозначен ABCDO и окрашен синим цветом).

5. Прямая, соответствующая целевой функции, на рисунке представлена пунктирной линией.

6. Прямую передвигаем параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка C. Это и есть точка, соответствующая оптимальному решению задачи.

7. Осталось вычислить координаты точки С. Она является точкой пересечения прямых (1) и (2). Решив совместно уравнения этих прямых, найдем: 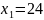, 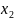. =4 .Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке f(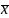 )=64 .

56. Свойства решений ЗЛП (4 теоремы):

— Теорема о выпуклости множества планов ЗЛП (Теорема №1)

— Теорема об угловой точке( Теорема №2)

— Теорема о соответствии опорному плану ЗЛП угловой точки многогранника решений ЗЛП (Теорема №3)

— Теорема о соответствии угловой точки опорного плана ( Теорема №4).

Основные теоремы линейного программирования

Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе.

Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора.

Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными).

Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

В частном случае, когда в систему ограничений входят только две переменные x1 и x2, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x1, x2 ≥ 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот.

Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений.

Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений.

57. Симплекс-метод, два этапа метода:

— Нахождение исходного опорного плана , канонический вид ЗЛП

— Симплекс-алгоритм.

Симплекс-метод – один из наиболее эффективных методов численного решения задач ЛП. Суть понятия «симплекс» заключается в следующем. Для тела в k -мерном пространстве симплексом называется множество, состоящее из k +1 вершин этого тела. Так, при k = 2, т.е. на плоскости, симплексом будут вершины треугольника; при k = 3 симплексом являются вершины четырехгранника, например тетраэдра, и т.д. Такое название методу дано по той причине, что в его основе лежит последовательный перебор вершин ОДЗП с целью определения координат той вершины, в которой функция цели имеет кстремальное значение.

Решение задачи с помощью симплекс-метода разбивается на два основных этапа. На первом этапе находят одно из решений, удовлетворяющее системе ограничений . Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных. При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными, или свободными переменными. Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получим базисное решение.

В системе из m уравнений с N неизвестными общее число базисных решений при N > m определяется числом сочетаний

Базисное решение, в котором все xi0, i = 1,m, называется допустимым базисным решением. Таким образом, первый этап решения, используя симплекс-метод, завершается нахождением допустимого базисного решения, хотя бы и неудачного.

На втором этапе производится последовательное улучшение найденного решения. При этом осуществляется переход от одного допустимого базисного решения к другому таким образом, чтобы значение целевой функции улучшилось. Процесс решения, используя симплекс-метод, продолжается до тех пор, пока не будет достигнуто наименьшее (или наибольшее) значение функции цели. Геометрически это означает переход по ребрам из одной вершины многогранника допустимых значений в другую по направлению к той, в которой значение функции цели достигает экстремума. Симплекс-метод дает оптимальную процедуру перебора базисных решений и обеспечивает сходимость к экстремальной точке за конечное число шагов. Используя симплекс-метод, вычисления на втором этапе ведутся по следующей схеме:

1) базисные переменные и функция цели выражаются через небазисные переменные;

2) по определенному правилу выбирается та из небазисных переменных, изменение значения которой способно улучшить значение F(x) , и она вводитя в базис;

3) определяется, какая из базисных переменных должна быть выведена из базиса, при этом новый набор базисных переменных, образующийся на каждом шаге, отличается от предыдущего только одной переменной;

4) базисные переменные и функция цели выражаются через новые небазисные переменные, и повторяются операции 2) и 3).

Если на определенном шаге в симплекс-методе окажется, что изменение значений любой из небазисных переменных не может улучшить F(x) , то последнее базисное решение оказывается оптимальным.

Рассмотрим пример, относящийся к задачам организационно-экономического управления и помогающий уяснить содержание симплекс-метода.

Пример 1. На приобретение оборудования для нового участка выделено 20 тыс. y.e. Оборудование должно быть размещено на площади, не превышающей 72 м^2. Может быть заказано оборудование двух видов: 1) оборудование стоимостью 5 тыс. y.e., занимающее площадь 6 м^2 и дающее 8 тыс. ед. продукции за смену; 2) оборудование стоимостью 2 тыс. y.e., занимающее площадь 12 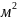и дающее за смену 4 тыс. ед. продукции. Найти оптимальный вариант приобретения оборудования, обеспечивающий максимум общей производительности участка, используя симплекс-метод.

Обозначим неизвестное количество оборудования первого и второго видов соответственно через x1 и x2. Функция цели может быть записана следующим образом: F(x) = 8x1 + 4x2(max). Ограничения по площади: 6x1 +12x2≤72; ограничения по стоимости: 5x1 + 2x2≤20 ; ограничения на знак переменных x1≥0 ; x2≥0.

Разделим коэффициенты первого из ограничений на 6 и приведем ограничения к виду равенств, вводя дополнительные переменные x3 и x4:

x1 + 2x2 + x3 =12, (1)

5x1 + 2x2 + x4 = 20 . (2)

Таким образом, ограничения задачи при решение симплекс-методом, приведены к системе из двух алгебраических уравнений с четырьмя неизвестными. Процедура решения задачи следующая:

1-й шаг. Для решения симплекс-методом выберем в качестве базисных переменных (БП) x2 и x4, так как определитель, составленный из коэффициентов при этих переменных в ограничениях задачи отличен от нуля.

Тогда x1 и x3 будут небазисными переменными (НП). Выразим базисные переменные и F(x) через небазисные.

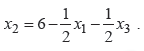(3)

Из второго ограничения следует, что

x4 = 20 - 2x2 - 5x1. (4)

С учетом выше приведенного выражения получим

x4 = 8 - 4x1 + x3. (5)

Тогда

F(x) = 8x1 + 4x2 = 24 + 6x1 - 2x3 . (6)

На каждом шаге решения задачи симплекс-методом НП приравниваются к нулю, следовательно, БП и F(x) будут равны свободным членам в соответствующих выражениях:

x1 = 0, x3 = 0, x2 = 6, x4 = 8, F(x) = 24.

Это решение соответствует координатам вершины A ОДЗП на рис. 1. Оптимальность решения проверяется по выражению F(x) для функции цели. Переменная x3 входит в это выражение с отрицательным коэффициентом; если вводить x3 в базис на следующем шаге, то она примет положительное значение, и от числа 24 некоторая величина будет вычитаться, т.е. значение F(x) уменьшится. Если же вводить в базис на следующем шаге x1, то значение функции цели увеличится, т.е. улучшится.

Применяя симплекс-метод, из базиса исключают ту переменную, которая раньше обратится в нуль при введении в базис x1. Анализируя (3) и (5), определяем, что из базиса следует исключить x4. На следующем шаге местами поменяются переменные x1 и x4.

2-й шаг симплекс-метода. x1 и x2 – базисные переменные, x3 и x4 – небазисные. Выразим базисные переменные и F(x) через небазисные переменные. Из (5) следует

x1=2+(1/4)x3-(1/4)x4 (7)

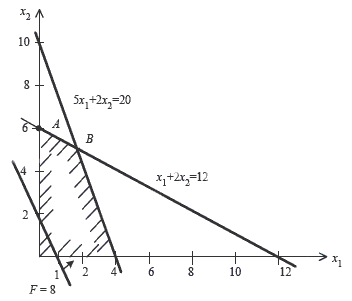
Рис. 1. Графическая интерпритация к примеру 1, используя симплекс-метод.

Подставив (7) в (3), получим

x2=5-(5/8)x3+(1/8)x4

Тогда F(x) = 8x1 + 4x2 = 36 - (1/2)x3 -(3/4)x4 . В результате x3 = x4 = 0 (как небазисные), x1 = 2, x2 = 5, F = 36 . Это решение соответствует координатам вершины В на рис. 1. Найденное решение симплекс-методом будет оптимальным, улучшить значение F(x) нельзя, так как переменные x3 и x4 входят в выражение для функции цели с отрицательными коэффициентами.

Таким образом, применяя симплекс-метод, нашли, что максимальная производительность участка 36 тыс. ед. продукции за смену будет обеспечена при закупке 2 ед. оборудования первого вида и 5 ед. оборудования второго вида. Дополнительные переменные x3 и x4 имеют смысл неиспользованных ресурсов. В данном примере все ресурсы по площади и по стоимости использованы полностью (x3 = x4 = 0).

Алгоритм симплекс-метода.

Рассмотрим решение ЗЛП симплекс-методом и изложим ее применительно к задаче максимизации.

1. По условию задачи составляется ее математическая модель.

2. Составленная модель преобразовывается к канонической форме. При этом может выделиться базис с начальным опорным планом.

3. Каноническая модель задачи записывается в форме симплекс-таблицы так, чтобы все свободные члены были неотрицательными. Если начальный опорный план выделен, то переходят к пункту 5.

Симплекс таблица: вписывается система ограничительных уравнений и целевая функция в виде выражений, разрешенных относительно начального базиса. Строку, в которую вписаны коэффициенты целевой функции F, называют F-строкой или строкой целевой функции.

4. Находят начальный опорный план, производя симплексные преобразования с положительными разрешающими элементами, отвечающими минимальным симплексным отношениям, и не принимая во внимание знаки элементов F-строки. Если в ходе преоб­разований встретится 0-строка, все элементы которой, кроме свободного члена, нули, то система ограничительных уравнений задачи несовместна. Если же встретится 0-строка, в которой, кроме свободного члена, других положительных элементов нет, то система ограничительных уравнений не имеет неотрицательных решений.

Приведение системы (2.55), (2.56) к новому базису будем называть симплексным преобразованием. Если симплексное преобра­зование рассматривать как формальную алгебраическую операцию, то можно заметить, что в результате этой операции происходит перераспределение ролей между двумя переменными, входящими в некоторую систему линейных функций: одна переменная из зависимых переходит в независимые, а другая наоборот - из независимых в зависимые. Такая операция известна в алгебре под названием шага жорданова исключения.

5. Найденный начальный опорный план исследуется на оптимальность:

а) если в F-строке нет отрицательных элементов (не считая свободного члена), то план оптимален. Если при этом нет и нулевых, то оптимальный план единственный; если же есть хотя бы один нулевой, то оптимальных планов бесконечное множество;

б) если в F-строке есть хотя бы один отрицательный элемент, которому соответствует столбец неположительных элементов, то <

в) если в F-строке есть хотя бы один отрицательный элемент, а в его столбце есть хотя бы один положительный, то можно перейти к новому опорному плану, более близкому к оптимальному. Для этого указанный столбец надо назначить разрешающим, по минимальному симплексному отношению найти разрешающую строку и выполнить симплексное преобразование. Полученный опорный план вновь исследовать на оптимальность. Описанный процесс повторяется до получения оптимального плана либо до установления неразрешимости задачи.

Столбец коэффициентов при переменной, включаемой в базис, называют разрешающим. Таким образом, выбирая переменную, вводимую в базис (или выбирая разрешающий столбец) по отрицательному элементу F-строки, мы обеспечиваем возрастание функции F.

Немного сложней определяется переменная, подлежащая исключению из базиса. Для этого составляют отношения свободных членов к положительным элементам разрешающего столбца (такие отношения называют симплексными) и находят среди них наименьшее, которое и определяет строку (разрешающую), содержащую исключаемую переменную. Выбор переменной, исключаемой из базиса (или выбор разрешающей строки), по минимальному симплексному отношению гарантирует, как уже установлено, положительность базисных компонент в новом опорном плане.

В пункте 3 алгоритма предполагается, что все элементы столбца свободных членов неотрицательны. Это требование не обязательно, но если оно выполнено, то все последующие симплексные преобразования производятся только с положительными разрешающими элементами, что удобно при расчетах. Если в столбце свободных членов есть отрицательные числа, то разрешающий элемент выбирают следующим образом:

1) просматривают строку, отвечающую какому-либо отрицательному свободному члену, например t-строку, и выбирают в ней какой-либо отрицательный элемент, а соответствующий ему столбец принимают за разрешающий (предполагаем, что ограничения задачи совместны);

2) составляют отношения элементов столбца свободных членов к соответствующим элементам разрешающего столбца, имеющим одинаковые знаки (симплексные отношения);

3) из симплексных отношений выбирают наименьшее. Оно и определит разрешающую строку. Пусть ею будет, например, р -строка;

4) на пересечении разрешающих столбца и строки находят разрешающий элемент. Если разрешающим оказался элемент y-строки, то после симплексного преобразования свободный член этой строки станет положительным. В противном случае на следующем шаге вновь обращаются к t-строке. Если задача разрешима, то через некоторое число шагов в столбце свободных членов не останется отрицательных элементов.

Нахождение исходного опорного плана , канонический вид ЗЛП

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования - симплексного метода или метода последовательного улучшения плана.

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение по отношению к цели задачи; до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако еще в 1939 г. идеи метода были разработаны российским ученым Л.В. Канторовичем.

Симплексный метод, позволяющий решить любую задачу линейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные примеры с применением симплексного метода можно решать и вручную.

Для реализации симплексного метода - последовательного улучшения решения - необходимо освоить три основных элемента:

• способ определения какого-либо первоначального допустимого базисного решения задачи;

• правило перехода к лучшему (точнее, не худшему) решению;

• критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.

В литературе достаточно подробно описываются: нахождение начального опорного плана (первоначального допустимого базисного решения), тоже - методом искусственного базиса, нахождение оптимального опорного плана, решение задач с помощью симплексных таблиц.

58. Основная теорема симплекс метода.

???????????????????????????????????????????????????????????????????????

59. Альтернативный оптимум в ЗЛП, вырожденность в ЗЛП.

Вырожденность в задачах линейного программирования

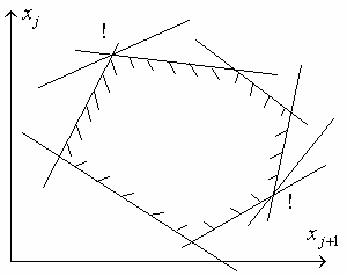
Рассматривая симплекс-метод, мы предполагали, что задача линейного программирования является невырожденной, т.е. каждый опорный план содержит ровно m положительных компонент, где m - число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения. Используя геометрическую интерпретацию для простейшего случая, когда n - m = 2 (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида xi = 0. Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку. Аналогично при n - m = 3 в вырожденной задаче в одной вершине пересекается более 3-х плоскостей xi = 0. В предположении о невырожденности задачи

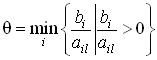
находилось только одно значение , по которому определялся индекс выводимого из базиса вектора условий (выводимой из числа базисных переменной). В

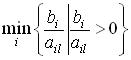
вырожденной задаче может достигаться на нескольких индексах сразу (для нескольких строк). В этом случае в находимом опорном плане несколько базисных переменных будут нулевыми. Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Это - так называемое явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явлеется довольно редким, возможность его не исключена. Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем "незначительного" изменения вектора правых частей системы ограничений на величины таким образом, чтобы задача стала невырожденной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи. Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления. Пусть переменную xj необходимо сделать базисной. Рассмотрим

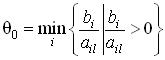
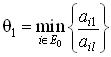множество индексов E0, состоящее из тех i, для которых достигается . Множество индексов i, для которых выполняется данное условие обозначим через E0,. Если E0, состоит из одного элемента, то из базиса исключается вектор условий Ai (переменная xi делается небазисной). Если E0 состоит более чем из одного элемента, то составляется множество E1, которое состоит из , на которых достигается . Если E1 состоит из одного индекса k, то из базиса выводится переменная xk. В противном случае составляется множество E2 и т.д. Практически правилом надо пользоваться, если зацикливание уже обнаружено.

Альтернативный оптимум в ЗЛП ???????????????????????????