39. Доминантная стратегия. Равновесие в доминантных стратегиях. Равновесие Нэша

Представим себе такую ситуацию, что целевая функция i-го игрока f_i(y) достигает максимума по его действию в точке, которая не зависит от действий других игроков. Это оптимальное действие, не зависящее от обстановки, называется доминантной стратегией агента. Формально: стратегия y_i^d будет доминантной стратегией, если какая бы обстановка не складывалась, его выигрыш будет максимальным при выборе именно доминантной стратегии:

Отметим, что в обеих частях неравенства фигурирует произвольная, но одна и та же обстановка.

Если у каждого игрока существует доминантная стратегия, то совокупность доминантных стратегий называется равновесием в доминантных стратегиях (РДС) . Это – идеальная ситуация для исследователя, описывающего математическую модель.

Гораздо чаще существует равновесие Нэша (РН). Джон Нэш, американский математик, в начале 50-х годов XX века предложил следующее: устойчивым исходом взаимодействия агентов можно считать такой вектор их действий, от которого в одиночку никому не выгодно отклоняться. Это значит, что ни один из агентов, в одиночку меняя свою стратегию на другую, не может увеличить свой выигрыш при условии, что остальные своих стратегий не меняют.

Формальное определение равновесия Нэша таково: , то есть для любого агента и для любого допустимого его действия выбор им равновесного по Нэшу действия дает ему выигрыш не меньший, чем при выборе любого другого действия при условии, что остальные игроки выбирают равновесные по Нэшу стратегии.

40. Иерархические игры. Простейшая модель иерархической игры. Критерии оптимизма и пессимизма

С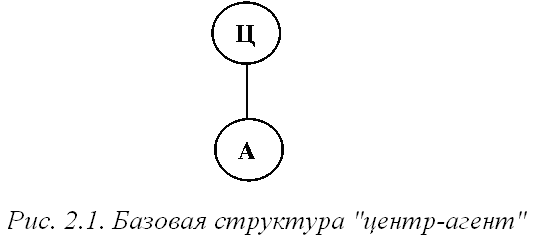 точки зрения управления наибольший интерес представляют модели игр, в которых агенты принимают решения не одновременно, а последовательно, то есть, если имеются управляющий орган и управляемые субъекты, то сначала начальник определяет правила игры, а дальше субъекты принимают решения, исходя из этих правил. Такие игры называются иерархическими. По определению, иерархическая игра – игра с фиксированной последовательностью ходов.

Простейшая модель иерархической игры – игра двух лиц, в которой первый (делающий первый ход) игрок – центр (управляющий орган), второй игрок – агент.

Пусть целевая функция центра Ф(u, y) зависит от выбираемого им действия и действия агента, и целевая функция агента зависит от тех же самых переменных. Предположим, что ситуация такова: центр выбрал своё действие и сообщил его агенту. Найдем множество тех действий, на которых достигается максимум целевой функции агента при фиксированном выборе центра: .

Исследование игры состоит в следующем – описать, каким образом будет вести себя агент, зная выбор центра. Типичных предположений два: критерии оптимизма и пессимизма.

Критерий оптимизма: агент настроен благожелательно к центру и выбирает из множества действий, которые максимизируют его целевую функцию, то действие, которое наиболее выгодно для центра.

Значит, оптимальным «управлением» (решением иерархической игры) будет действие центра, которое доставляет максимум по множеству допустимых управлений от его выигрыша Ф(u, y) , в который подставлен максимум по множеству реакций агента:

Критерий пессимизма: агенту все равно, как действовать, поэтому центр будет ориентироваться на наихудший случай. Тогда решение следующее:

Т.е., центр вычисляет минимум своей целевой функции по действию агента из множества P(u), а дальше максимизирует выбором своего действия.