7.3. Массовые содержания ерэ и урановый эквивалент

Обозначим содержание j-го излучателя в единице объема породы через Q_j, и соответствующее число испускаемых с энергией E гамма-квантов через S_j(E). Если излучатели равномерно заполняют все пространство, то интенсивность излучения J(E) на основании формулы (7.9) равна

(7.13)

где  – массовый коэффициент ослабления; q_j=Q_j/ – массовое содержание излучателя. В выражении (7.10) индекс j пробегает значения j=1 (⁴⁰К), j=2 (U+Ra с продуктами распада), j=3 (Th с продуктами распада).

Обратим внимание на то, что вследствие комптоновского механизма взаимодействия показания интегрального канала (ГМ) определяются не объемными, а массовыми содержаниями естественно-радиоактивных элементов (ЕРЭ).

Пусть интегральный канал ГМ скважинного радиометра (ННМ, НГМ, ГГМ, ИННМ, ИНГМ) регистрирует гамма-кванты со спектральной эффективностью (E), тогда показание прибора J будет

(7.14)

где

(7.15)

Величина С_j называется концентрационной чувствительностью (для j-го радионуклида) и определяет показание, соответствующее единице массового содержания j-го радионуклида (вместе с продуктами распада в состоянии радиоактивного равновесия), в однородной безграничной среде (или необсаженной сухой скважине).

Ни число распадов (активность), ни мощность экспозиционной дозы не характеризуют однозначно содержания ЕРЭ в породе и не обеспечивают сопоставимости результатов лабораторных и скважинных измерений.

При неспектрометрических измерениях по показаниям канала ГМ невозможно выделять гамма-излучение различных излучателей и количественно оценить содержание каждого из них в отдельности. Единственная возможность количественной интерпретации данных интегрального ГМ состоит в оценке суммарного содержания ЕРЭ в определенных единицах. Такими единицами могут быть эквивалентные массовые содержания отдельных радионуклидов, т. е. такие содержания, которым соответствуют одинаковые показания интегрального канала.

Допустим, что в однородной безграничной среде, окружающей прибор, равномерно распределен j-й излучатель с единичной массовой концентрацией q_j =1. Определим эквивалентное по показаниям содержание урана eU_j («урановый эквивалент j-го излучателя»):

J = C_j [1]  C_U eU_j (7.16)

Откуда

eU_j = C_j / C_U ; [eU_j] = [q_j] (7.17)

Аналогично можно ввести калиевый (еK_j) и ториевый (eТh_j) эквиваленты:

eK_j = C_j / C_K ; eТh_j = C_j / C_Th

За единицу уранового эквивалента примем массовое содержание урана 10^–4 % (эта величина получила обозначение ur):

10^–4 % U = 1eU_U  1ur.

В разведке на уран эта величина является искомой величиной. Однако для изучения коллекторов нефти и газа, содержания ЕРЭ в которых сравнительно невелики, ее применение требует обоснования. Из определений (7.15) – (7.16) следует, что величина eU_j (или eK_j, eTh_j) определяет массовое содержание урана (калия, тория), которому соответствует такое же показание канала, как и для единичного массового содержания j-го излучателя:

1 % K  1eU_K = C_K / C_U , ur 10^–4 % Th  1eU_Th = C_Th / C_U, ur

На основании (7.16) и (7.17) урановый эквивалент eU суммарного содержания ЕРЭ определяет такое массовое содержание урана, при котором показание канала в однородной безграничной среде такое же, как при данном содержании ЕРЭ в их природной смеси:

. (7.18)

Для определения концентрационных чувствительностей С_j необходимо выполнить измерения в четырех моделях пластов – «фоновой», «калиевой», «урановой», «ториевой» (для контроля дополнительно проводятся измерения в модели со смесью излучателей). Тогда на основании (7.15) получаем систему уравнений, разрешимую относительно С_j. Измерения выполняются в специальных моделях пластов, прошедших государственную аттестацию в качестве стандартных образцов содержаний ЕРЭ.

Используя определения (7.15) и (7.17), можно показать, что в отличие от С_j, значения eU_j должны быть устойчивыми относительно изменений конструкционных параметров аппаратуры.

Экспериментальные данные подтверждают, что для различных типов аппаратуры значения С_j изменяются в широком диапазоне, однако соответствующие эквиваленты eU_j остаются практически постоянными. Это означает, что для довольно широкого класса аппаратуры (интегральный канал приборов с диаметром более 6 см, предназначенных для исследования разрезов нефтегазовых скважин) параметр eU_j(eK_j, eTh_j) переходит из разряда метрологических в разряд физических. Независимо от типа аппаратуры урановый эквивалент eU вычисляется по известным содержаниям {q_j} по правилу (7.18):

eU = 1,79q_K [%] + q_U [10^–4 %] + 0,39q_Th [10^–4 %].

Оценим вклады  _j различных излучателей (К, U, Th) в результирующие показания канала интегрального ГМ:

,

где eU определяется выражением (7.18). Полагая q_j = const, находим:

.

Используя численные значения eU_j, легко оценить, что вклад калия составляет около 60%, а равновесных урана и тория – соответственно 30 и 10%.

Петрофизическая модель гамма-метода. Переход к определению суммарного содержания ЕРЭ в единицах уранового эквивалента позволяет строго сформулировать петрофизическую модель ГМ в виде

; ; (7.19)

где  – плотность породы; _i, eU_i, K_i – соответственно минералогические плотности, урановые эквиваленты и объемные содержания компонент. Эта модель включается в систему уравнений комплексной петрофизической интерпретации данных ГМ (в комплексе с другими методами ГИС).

Из петрофизической модели (7.16) следует, что, значения eU существенно зависят от множества факторов, причем эти зависимости (в частности, от содержания и типа глинистого цемента) в коллекторах различного типа могут существенно различаться. Однако в шкале относительной глинистости h=К_гл/(К_п + К_гл), нормированной на ее максимальное значение h* = h/h_max

h* = h/h_max , где h_max=1—/М

( - полная флюидоудерживающая способность коллектора, М – пористость матрицы) двойной разностный параметр

DeU(h*) =[eU(h*)eU(0)]/[eU(1)eU(0)], (7.20)

очень слабо зависит от параметра М (скелетной пористости) и практически не зависит от соотношения радиоактивностей матрицы и цемента. Для различных значений М мы имеем семейство нелинейных кривых (Рис.7.4) DeU(h*). При неизменных диаметре скважины и свойствах промежуточных зон выполняется равенство DeU = DJ_g , где DJ_g — обычный двойной разностный параметр ГМ

J_ =(JJ_min)/(J_maxJ_min), d_скв. = const. (7.21)

Таким образом, из петрофизической модели ГМ для гранулярного коллектора вытекает, что параметр DeU определяется величиной нормированной эффективной пористости  (нормированной относительной глинистости *). Следовательно, ГМ (ГМ-С) является одновременно и «методом относительной глинистости», и «методом эффективной пористости».

Р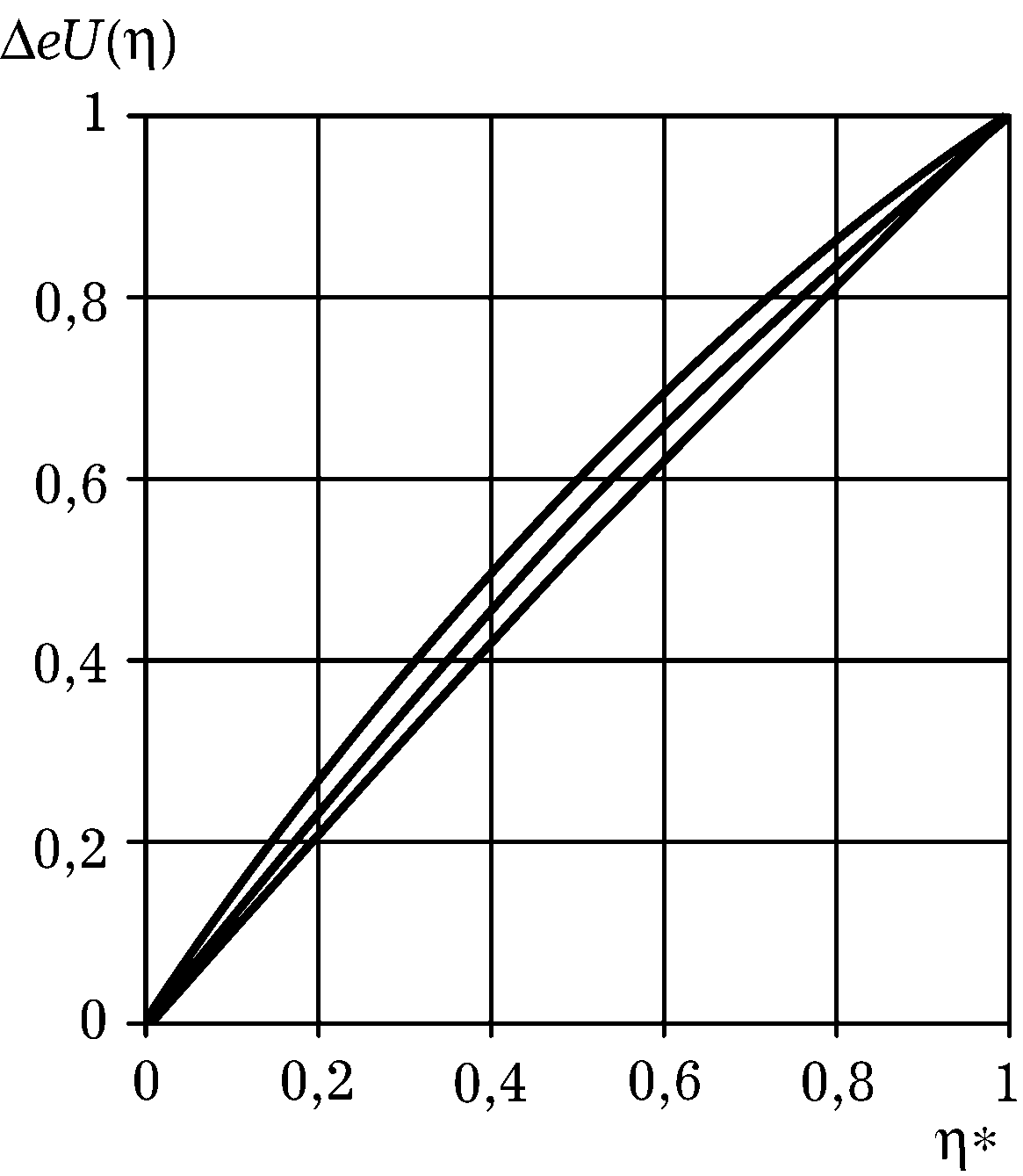 ис.7.4. Зависимости двойного разностного параметра по урановому эквиваленту от нормированной относительной глинистости при различных значениях скелетной пористости (шифр кривых, %).

Можно указать, по крайней мере, три признака применимости ГМ для определения эффективной пористости. Каждый из этих признаков состоит в наличии значимой корреляции между:

1) диаграммами ГМ и ПС (при отсутствии данных ГМ-С):

2. содержаниями калия, урана и тория;

3. содержаниями калия и тория при относительно низком содержании урана (признаки 2 и 3 — при наличии данных ГМ-С).

В сложных терригенных полиминеральных глинистых коллекторах условия применимости интегрального гамма-метода (ГМ) для определения эффективной пористости не выполняются. Применение гамма-спектрометрии (ГМ-С) существенно расширяет область применимости метода естественной радиоактивности, в частности, на случай полиминеральных глинистых коллекторов.