
- •1.Тепловая машина,термический кпд.Холодильная машина,холодильный коэффициент. Вечный двигатель 1 и 2 рода.
- •2.Цикл Карно.Pv и ts диаграммы,кпд цикла Карно.
- •3.Цикл одноступенчатого компрессора.Работа сжатия газа в компрессоре.
- •6.Цикл газотурбинной установки.
- •7.Теплопередачи.Основные виды передачи теплоты. Температурное поле,градиент температуры, тепловой поток. Закон Фурье. Коэффициент теплопроводности.
- •8.Диф.Уравнение теплопроводности. Коэффициент температуропроводности.Уравнение Пуассона,уравнение Лапласа.
- •10.Теплопроводность при стационарном режиме.Передача теплоты через плоскую стенку.Многослойная стенка.
- •11.Однородная цилиндрическая стенка.Критический диамерт изоляции.
- •12.Основы теории подобия физических явлений.
- •14) Теория подобия для обобщения опытных данных.
- •16. Теплопередача при внешнем обтекании тел.
- •19) Основные законы теплового излучения
- •3) Закон смещения Вина - даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела. Общий вид закона смещения Вина
- •20) Теплообмен между двумя поверхностями
- •1) Теплообмен излучением между двумя плоскими параллельными пластинами.
12.Основы теории подобия физических явлений.
-При изучении различных физических явлений применяют два метода исследований,которые позволяют получить количественные закономерности для исследуемых явлений.В первом методе используют экспериментальное изучение конкретных свойств,единичного явления,во втором исходят из теоретического исследования рассматриваемой проблемы.Достоинством экспериментального метода исследования является достоверность получаемых результатов.Кроме того при выполнении эксперимента основное внимание можно сосредоточить на изучении величин,представляющих наибольший практический интерес.Основной недостаток экспериментально метода исследования заключается в том,что результаты данного эксперимента не могут быть использовании применительно к другому явлению,которое в деталях отличается от изученного.Второй медот ислледования для нахожденеия количественных зависимостей,который широко применяется современной наукой,рассматривается в математической или теоретической физике.При выводе диф.уравнений теоретической физики используется самые общие законы природы,которые в свою очередь являются результатом чрезвычайно широкого обобщения опытных данных.Любое диф.уравнение или система является математической моделью целого класса явлений.Под классом понимается такая совокупность явлений,которая характеризуется одинаковым механизмом процессов и одинаковой физической природой.Если положительные стороны математического и экспериментального методов исследования объединить в одно целое,то можно получть универсальный аппарат для изучения различенных явлений природы.Такое объединение обоих методов осуществляется теорией подобия.
14) Теория подобия для обобщения опытных данных.
При постановке любого эксперимента всегда необходимо заранее знать: 1) какие величины надо измерять в опыте; 2) как обрабатывать результаты опыта; 3) какие явления подобны изучаемому. На эти вопросы ответ содержится в изложенных выше трех теоремах подобия. На первый вопрос отвечает первая теорема: в опытах нужно измерять все величины, содержащиеся в числах подобия изучаемого процесса. На второй вопрос отвечает вторая теорема: результаты опыта следует обрабатывать в числах подобия и зависимость между ними представлять в виде уравнений подобия; это позволяет найти общую закономерность, справедливую для всех процессов, подобных изучаемому. На третий вопрос ответ дает третья теорема; подобны те явления, у которых подобны условия однозначности и равны определяющие числа подобия (критерии подобия). Благодаря этим ответам теория подобия по существу является теорией эксперимента.
16. Теплопередача при внешнем обтекании тел.
Интегральные
уравнения теплового и динамического
пограничных слоев при безнапорном
обтекании пластины.
Рассмотрим
участок плоской поверхности, с температурой
tw
и омывается
потоком несжимаемой жид-ти с темп. tf.
Ширина поверхности равна 1. на расстоянии
х от начала координат выделим элемент
теплового пограничного слоя ABCD
длиной dx
(две боковые поверхности элемента
образованы вертикальными плоскостями,
нормальными к оси х). Тепловой баланс
этого элемента при стационарных условиях
теплообмена и отсутствии в жидкости
внутренних источников теплоты: Qx
– Qx+dx+dQ’x=
dQ’’x.
Два первых члена определяют изменение
энтальпии теплоносителя при течении
его между поверх-ми АВ и CD,
третий - подвод теплоты вместе с
теплоносителем, поступивший через
поверх-ть ВС. Правая часть уравнения
отражает теплообмен между поверхностью
и теплоносителем.
Величину Qx+dx
найдем
разложением Qx
в ряд
Тейлора: Qx+dx=
Qx+(d
Qx/dx)dxПренебрегая
распространением теплоты вдоль оси х
найдем : Qx= где
wx
– переменная по толщине пограничного
слоя скорость потока.dQ’x=сptfdG’x,
G’x
– массовый расход вещества через
поверхность ВС. dQ’x=
где
wx
– переменная по толщине пограничного
слоя скорость потока.dQ’x=сptfdG’x,
G’x
– массовый расход вещества через
поверхность ВС. dQ’x= теплота,
проходящая через поверхность теплообмена:
dQ’’x=qdx.Подставим
все выражения в первую формулу:
теплота,
проходящая через поверхность теплообмена:
dQ’’x=qdx.Подставим
все выражения в первую формулу:
 Считая,
что теплофизические характеристики
теплоносителя от температуры не зависят,
выражение примет вид:
Считая,
что теплофизические характеристики
теплоносителя от температуры не зависят,
выражение примет вид:
 .
Подставив в это выражение тепловую
нагрузку из уравнения Фурье, в котором
температурный градиент взят по абсолютной
величине, получим:
.
Подставив в это выражение тепловую
нагрузку из уравнения Фурье, в котором
температурный градиент взят по абсолютной
величине, получим:
 Это уравнение называется интегральным
уравнением для теплового пограничного
слоя. Аналогично выводится уравнение
для динамического пограничного слоя,
(интегральное соотношением количества
движения):
Это уравнение называется интегральным
уравнением для теплового пограничного
слоя. Аналогично выводится уравнение
для динамического пограничного слоя,
(интегральное соотношением количества
движения):
![]() ,
,
где t – напряжение трения на поверхности теплообмена, δ - толщина потери импульса.
Т еплоотдача
пластины при ламинарном пограничном
слое. Решение на основе теории динамического
погр. слоя.
Зададим
форму профиля скоростей в пограничном
слое степенным многочленом:
еплоотдача
пластины при ламинарном пограничном
слое. Решение на основе теории динамического
погр. слоя.
Зададим
форму профиля скоростей в пограничном
слое степенным многочленом:
![]() Для оценки коэффициентов используем
граничные условия: при у=0, w=0
и
Для оценки коэффициентов используем
граничные условия: при у=0, w=0
и
![]() ;
при у=δ,
;
при у=δ,
![]() и
и
![]() .
Подставив в формулу получим а0=0, а1=3/2,
а2=0, а3=-1/2
Следовательно, многочлен
перепишется так:
.
Подставив в формулу получим а0=0, а1=3/2,
а2=0, а3=-1/2
Следовательно, многочлен
перепишется так:
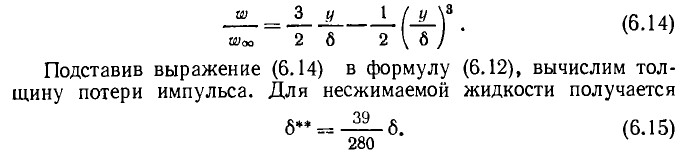 (звездочки
писать не надо)
(звездочки
писать не надо)


Теплоотдача при внешнем обтекании труб.
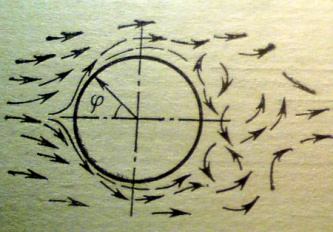
Течение при
обтекании поперечной трубы.
На
фронтовой части трубы образуется
пограничный слой, толщина которого
достигается наибольшей величины вблизи
ϕ=90˚.
В этой зоне происходит отрыв потока от
поверхности и кормовая часть трубы
омывается сильно завихренным потоком
с обратными
циркуляционными токами.
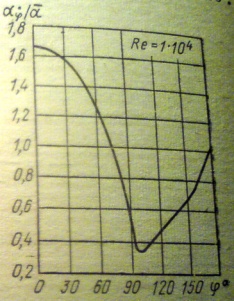
Показана типичная
зависимость
отношения местного коэффициента
теплоотдачи αф к среднему его значению
для всей трубы от угла , который определяет
местоположение точки на окружности.
Теплоотдача протекает наиболее интенсивно
вблизи лобовой образующей цилиндра. В
местах, где ламинарный пограничный слой
достигает наибольшей толщины, коэффициент
теплоотдачи имеет минимальное значение.
Средняя теплоотдача трубы определяется
уравнением, полученным экспериментальным
путем : (1)
 в
котором при Ref
в
котором при Ref![]() c=0,56
и n=0,5,
а при Ref
c=0,56
и n=0,5,
а при Ref![]() c=0,28
и n=0,6.
За определяющий размер в этом уравнении
принят диаметр трубы, а критерий Re
вычисляется по скорости невозмущенного
потока. Если направление движения потока
составляет с осью трубы угол отличный
от 90°, то коэффициент теплоотдачи,
определенный по формуле, надо умножить
на поправку εψ
числовое
значение которой приводится в справочниках.
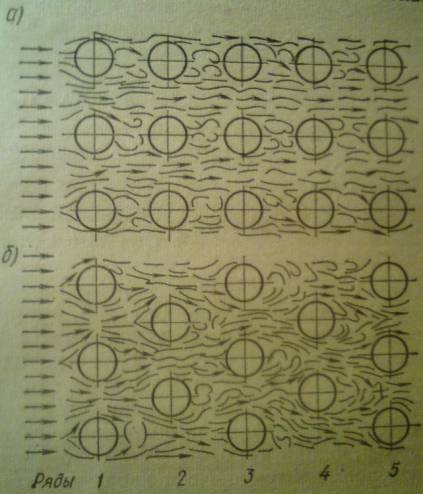
При ψ<90 то εψ<1. Теплоотдача труб,
составляющих трубный пучок, зависит от
расположения труб в пучке, а также от
номера ряда, в котором труба находится.
Характер движения теплоносителя а-
коридорный, б – шахматный.
При
шахматном расположении труб теплоноситель
перемешивается лучше, и теплообмен
протекает более интенсивно. Первый ряд
труб омывается невозмущенным потоком
жидкости и потому этот ряд имеет
наименьший коэффициент теплоотдачи. В
последующих рядах труб теплоотдача
протекает более интенсивно, можно
считать, что третий и последующие ряды
труб имеют одинаковый средний коэффициент
теплоотдачи. Если в качестве определяющего
размера выбрать диаметр трубы, а критерий
Re подсчитывать по скорости в наиболее
узком сечении пучка (в сечении, где
расположены трубы), то независимо от
расстояния между трубами коэффициент
теплоотдачи третьего и последующего
рядов труб можно определять по уравнению
(1). Числовые значения коэффициентов с
и n
зависят от вида пучка. При Ref
<< 103
для обоих видов пучков труб
с = 0,56,
n=
0,5. При Ref
> > 103 для
коридорного пучка с = 0,22, n
= 0,65, для шахматного с = 0,4, n
= 0,6.
Коэффициенты теплоотдачи первого
и второго рядов подсчитываются через
коэффициент теплоотдачи третьего ряда.
Для коридорного расположения труб: а1
= 0,6а3; а2 = 0.9а3; Для шахматного расположения
труб: а1 = 0,6а3; а2 = 0,7а3. Когда направление
скорости потока составляет с осью труб
угол ψ < 90°, рассчитанный по формуле
коэффициент теплоотдачи надо
скорректировать поправкой εψ.
Закономерности теплоотдачи зависят от
формы сечения поперечно обтекаемого
тела и от ориентировки тела по отношению
к набегающему потоку. Уравнения подобия
для тел с различной формой поперечного
сечения приводятся в справочной
литературе.
c=0,28
и n=0,6.
За определяющий размер в этом уравнении
принят диаметр трубы, а критерий Re
вычисляется по скорости невозмущенного
потока. Если направление движения потока
составляет с осью трубы угол отличный
от 90°, то коэффициент теплоотдачи,
определенный по формуле, надо умножить
на поправку εψ
числовое
значение которой приводится в справочниках.
При ψ<90 то εψ<1. Теплоотдача труб,
составляющих трубный пучок, зависит от
расположения труб в пучке, а также от
номера ряда, в котором труба находится.
Характер движения теплоносителя а-
коридорный, б – шахматный.
При
шахматном расположении труб теплоноситель
перемешивается лучше, и теплообмен
протекает более интенсивно. Первый ряд
труб омывается невозмущенным потоком
жидкости и потому этот ряд имеет
наименьший коэффициент теплоотдачи. В
последующих рядах труб теплоотдача
протекает более интенсивно, можно
считать, что третий и последующие ряды
труб имеют одинаковый средний коэффициент
теплоотдачи. Если в качестве определяющего
размера выбрать диаметр трубы, а критерий
Re подсчитывать по скорости в наиболее
узком сечении пучка (в сечении, где
расположены трубы), то независимо от
расстояния между трубами коэффициент
теплоотдачи третьего и последующего
рядов труб можно определять по уравнению
(1). Числовые значения коэффициентов с
и n
зависят от вида пучка. При Ref
<< 103
для обоих видов пучков труб
с = 0,56,
n=
0,5. При Ref
> > 103 для
коридорного пучка с = 0,22, n
= 0,65, для шахматного с = 0,4, n
= 0,6.
Коэффициенты теплоотдачи первого
и второго рядов подсчитываются через
коэффициент теплоотдачи третьего ряда.
Для коридорного расположения труб: а1
= 0,6а3; а2 = 0.9а3; Для шахматного расположения
труб: а1 = 0,6а3; а2 = 0,7а3. Когда направление
скорости потока составляет с осью труб
угол ψ < 90°, рассчитанный по формуле
коэффициент теплоотдачи надо
скорректировать поправкой εψ.
Закономерности теплоотдачи зависят от
формы сечения поперечно обтекаемого
тела и от ориентировки тела по отношению
к набегающему потоку. Уравнения подобия
для тел с различной формой поперечного
сечения приводятся в справочной
литературе.
17.Теплопроводность твердых тел
Теплопроводностью
называется процесс переноса тепла от
более нагретых частей тела к менее
нагретым, приводящий к выравниванию
температуры тела. В твердых телах, в
отличие от жидкостей и газов, невозможна
конвекция (передача тепла потоками
нагретого вещества), поэтому перенос
тепла осуществляется только за счет
колебаний кристаллической решетки
или с точки зрения квантовой теории
за счет движения фононов. Если при
данной температуре T один из
узлов колеблется с амплитудой u,
большей среднего значения |
|
где λ коэффициент
теплопроводности, который численно
равен количеству тепла, прошедшего
через единицу площади за единицу времени
при градиенте температуры, равном
единице (площадка
перпендикулярна
оси x). В системе СИ размерность
коэффициента теплопроводности составляет
Вт/(м×К), но часто используют размерности
Вт/(см×К) и кал/(см×с×К). Знак минус в
формуле (6.53) показывает, что распространение
тепла идет в сторону выравнивания
градиента температуры (от более нагретой
части тела к менее нагретой). При низких
температурах следует учитывать квантовый
характер тепловых волн. Если ![]() ,
то при теплообмене возбуждаются любые
колебания в кристалле, все квантовые
переходы возможны, и поэтому квантовый
характер явления теплообмена не заметен.
При низких температурах, когда
,
то при теплообмене возбуждаются любые
колебания в кристалле, все квантовые
переходы возможны, и поэтому квантовый
характер явления теплообмена не заметен.
При низких температурах, когда ![]() ,
в кристалле возбуждены лишь колебания
с малыми частотами, и большие энергетические
ступеньки не могут быть преодолены
возникающими тепловыми «толчками».
Рассмотрим процесс передачи тепла на
основе представлений о фотонах.
Из
теории Дебая следует, что возбужденное
состояние решетки можно представить
как идеальный газ фононов, свободно
движущийся в объеме кристалла. Фононный
газ в определенном интервале температур
ведет себя подобно идеальному газу, а
поскольку фононы являются основными
переносчиками тепла в твердом теле (это
утверждение справедливо только для
диэлектриков), то коэффициент
теплопроводности твердого тела можно
выразить такой же зависимостью, как
коэффициент теплопроводности идеального
газа
,
в кристалле возбуждены лишь колебания
с малыми частотами, и большие энергетические
ступеньки не могут быть преодолены
возникающими тепловыми «толчками».
Рассмотрим процесс передачи тепла на
основе представлений о фотонах.
Из
теории Дебая следует, что возбужденное
состояние решетки можно представить
как идеальный газ фононов, свободно
движущийся в объеме кристалла. Фононный
газ в определенном интервале температур
ведет себя подобно идеальному газу, а
поскольку фононы являются основными
переносчиками тепла в твердом теле (это
утверждение справедливо только для
диэлектриков), то коэффициент
теплопроводности твердого тела можно
выразить такой же зависимостью, как
коэффициент теплопроводности идеального
газа
|
(6.54) |
где ![]() −
теплоемкость единицы объема фононного
газа,
−
теплоемкость единицы объема фононного
газа, ![]() −
средняя длина свободного пробега
фонона,
−
средняя длина свободного пробега
фонона, ![]() −
скорость распространения звука в данном
теле.
−
скорость распространения звука в данном
теле.
Вычисление средней
длины свободного пробега фонона
представляет собой сложную задачу,
поскольку она зависит от того, на чем
происходит рассеяние фононов: на других
фононах, на дефектах структуры или на
внешних гранях образца. Однако
теоретический анализ приводит к тому,
что при достаточно высоких температурах
средняя длина свободного пробега фонона
обратно пропорциональна абсолютной
температуре. Поэтому коэффициент
теплопроводности твердых тел при
температурах выше характеристической
(![]() )
обратно пропорционален абсолютной
температуре.
)
обратно пропорционален абсолютной
температуре.
В
достаточно чистых и бездефектных
кристаллах при температуре, близкой к
абсолютному нулю, возникает зависимость
средней длины свободного пробега фононов
от размеров образца. Это объясняется
тем, что при низких температурах
концентрация фононов мала, а следовательно,
мала вероятность рассеяния фононов на
других фононах. Полагая среднюю длину
свободного пробега фононов приблизительно
равной линейным размерам кристалла (![]() ,
где L −
линейный размер кристалла), можно
уравнение (6.54) переписать в виде
,
где L −
линейный размер кристалла), можно
уравнение (6.54) переписать в виде
|
(6.55) |
В
правой части уравнения (6.55) от температуры
зависит только теплоемкость единицы
объема фононного газа
.
При температурах, близких к абсолютному
нулю, теплоемкость пропорциональна ![]() ,
поэтому и коэффициент теплопроводности λ
пропорционален
кубу абсолютной температуры. Такой
вывод подтверждается экспериментальными
данными.
,
поэтому и коэффициент теплопроводности λ
пропорционален
кубу абсолютной температуры. Такой
вывод подтверждается экспериментальными
данными.
Анизотропия сил связи в кристаллах приводит к анизотропии коэффициента теплопроводности.
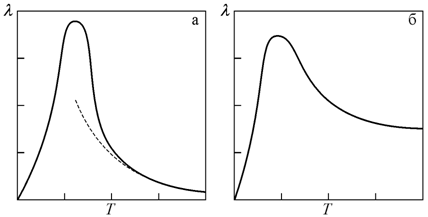 В
диэлектриках, практически не имеющих
свободных электронов, перенос тепла
осуществляется только фононами. Выше
было сказано, что средняя длина свободного
пробега
зависит
от процессов рассеяния фононов на
различных объектах. Все это приводит к
тому, что температурная зависимость
коэффициента теплопроводности λ для
диэлектриков имеет вид кривой с
максимумом. Левая восходящая ветвь
зависимости обусловлена увеличением
числа фононов с ростом температуры, а
правая нисходящая связана с ослабляющими
фонон-фононным и другими видами рассеяния.
Вид зависимости λ
(T)
для металлов (рис. 6.12, б)
качественно похож на кривую для
диэлектриков. Это связано с преобладанием
при очень низких температурах фононного
механизма теплопередачи. Однако с ростом
температуры вклад фононной составляющей
в этот процесс становится пренебрежимо
мал и теплопередача осуществляется в
основном свободными электронами. При
относительно высоких температурах в
металлах коэффициент теплопроводности
λ практически
перестает изменяться с увеличением Т.
В
диэлектриках, практически не имеющих
свободных электронов, перенос тепла
осуществляется только фононами. Выше
было сказано, что средняя длина свободного
пробега
зависит
от процессов рассеяния фононов на
различных объектах. Все это приводит к
тому, что температурная зависимость
коэффициента теплопроводности λ для
диэлектриков имеет вид кривой с
максимумом. Левая восходящая ветвь
зависимости обусловлена увеличением
числа фононов с ростом температуры, а
правая нисходящая связана с ослабляющими
фонон-фононным и другими видами рассеяния.
Вид зависимости λ
(T)
для металлов (рис. 6.12, б)
качественно похож на кривую для
диэлектриков. Это связано с преобладанием
при очень низких температурах фононного
механизма теплопередачи. Однако с ростом
температуры вклад фононной составляющей
в этот процесс становится пренебрежимо
мал и теплопередача осуществляется в
основном свободными электронами. При
относительно высоких температурах в
металлах коэффициент теплопроводности
λ практически
перестает изменяться с увеличением Т.
18) Тепловое излучение или лучеиспускание — передача энергии от одних тел к другим в виде электромагнитных волн за счёт их тепловой энергии. Тепловое излучение в основном приходится на инфракрасный участок спектра, т.е на длины волн от 0,74 мкм до 1000 мкм. Отличительной особенностью лучистого теплообмена является то, что он может осуществляться между телами, находящимися не только в какой-либо среде, но и вакууме.
Основные свойства теплового излучения:
- Тепловое излучение происходит по всему спектру частот от нуля до бесконечности
- Интенсивность теплового излучения неравномерна по частотам и имеет явно выраженный максимум при определенной частоте
- C ростом температуры общая интенсивность теплового излучения возрастает
- C ростом температуры максимум излучения смещается в сторону больших частот (меньших длин волн)
- Тепловое излучение характерно для тел независимо от их агрегатного состояния
- Отличительным свойством теплового излучения является равновесный характер излучения. Это значит , что если мы поместим тело в термоизолированный сосуд, то количество поглощаемой энергии всегда будет равно количеству испускаемой энергии.
Основные понятия и характеристики теплового излучения:
Энергетическая
светимость тела -
![]() —
физическая величина, являющаяся функцией
температуры и численно равная энергии,
испускаемой телом в единицу времени с
единицы площади поверхности по всем
направлениям и по всему спектру
частот.
—
физическая величина, являющаяся функцией
температуры и численно равная энергии,
испускаемой телом в единицу времени с
единицы площади поверхности по всем
направлениям и по всему спектру
частот.![]() ;
; ![]() Дж/с·мІ
= Вт/мІ
Дж/с·мІ
= Вт/мІ
Спектральная
плотность энергетической светимости —
функция частоты и температуры,
характеризующая распределение энергии
излучения по всему спектру частот (или
длин волн).![]()
Аналогичную
функцию можно написать и через длину
волны![]()
Можно доказать, что спектральная плотность энергетической светимости, выраженная через частоту и длину волны, связаны соотношением:
Поглощающая
способность тела — ![]() —
функция частоты и температуры,
показывающая, какая часть энергии
электромагнитного излучения, падающего
на тело, поглощается телом в области
частот
—
функция частоты и температуры,
показывающая, какая часть энергии
электромагнитного излучения, падающего
на тело, поглощается телом в области
частот ![]() вблизи
вблизи ![]()
![]()
где ![]() —
поток энергии, поглощающейся телом.
—
поток энергии, поглощающейся телом.
![]() —
поток энергии,
падающий на тело в области
вблизи
—
поток энергии,
падающий на тело в области
вблизи
Отражающая
способность тела — ![]() —
функция частоты и температуры, показывающая
какая часть энергии электромагнитного
излучения, падающего на тело, отражается
от него в области частот
вблизи
—
функция частоты и температуры, показывающая
какая часть энергии электромагнитного
излучения, падающего на тело, отражается
от него в области частот
вблизи
![]()
где ![]() —
поток энергии, отражающейся от тела.
—
поток энергии, отражающейся от тела.
— поток энергии, падающий на тело в области вблизи
Абсолютно
черное тело —
это физическая абстракция (модель), под
которой понимают тело, полностью
поглощающее всё падающее на него
электромагнитное излучение
![]() —
для абсолютно черного тела
—
для абсолютно черного тела
Серое тело — это такое тело, коэффициент поглощения которого не зависит от частоты, а зависит только от температуры
![]() —
для серого тела
—
для серого тела
Объемная
плотность энергии излучения — ![]() —
функция температуры, численно равная
энергии электромагнитного излучения
в единицу объема по всему спектру частот
—
функция температуры, численно равная
энергии электромагнитного излучения
в единицу объема по всему спектру частот
Спектральная
плотность энергии — ![]() —
функция частоты и температуры, связанная
с объемной плотностью излучения
формулой:
—
функция частоты и температуры, связанная
с объемной плотностью излучения
формулой:![]()
Следует
отметить, что спектральная плотность
энергетической светимости для абсолютно
черного тела связана со спектральной
плотностью энергии следующим
соотношением:![]() —
для абсолютно черного тела
—
для абсолютно черного тела
