8.Диф.Уравнение теплопроводности. Коэффициент температуропроводности.Уравнение Пуассона,уравнение Лапласа.

-При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:внутренние источники теплоты отсутствуют,тело однородно и изотропно, используется закон сохранения энергии,который для данного случая формулируется как»разность между количеством теплоты,вошедшей вследствие теплопроводности в элементарный паралепипед за время dt и вышедший из него за тоже время,расходуется на изменение внутренней энергии рассматриваемого элементарного объема.После преобразований получаем это уравнение -называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности.

; -диф.уравнение теплопроводности с источниками теплоты внутри тела.qv-количество выделяемой теплоты в единице объема вещества в единицу времени,вт/м^2,с-массовая теплоемкость,дж/(кг*град),р-плотность,кг/м^3

- Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания) температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянном давлении, в системе СИ измеряется в м²/с. где a— температуропроводность, — теплопроводность, Ср— изобарная удельная теплоёмкость,ρ— плотность

-Это дифференциальное уравнение носит название уравнения Пуассона. -оператор Лапласса.

9.Краевые условия.

краевые условия задают начальное распределение температуры в заданной расчетной области и условия теплообмена на границе этой области .

Начальные Условия имеют вид: Т (х, 0) = Т₀ = const.

_{При граничных условиях I рода задают значение температуры на границе расчетной области.}

При граничных условиях II рода задают значение плотности теплового потока на границе расчетной области.

При граничных условиях III рода задают температуру внешней среды, окружающей тело, и закон теплообмена между средой и поверхностью тела.

С учетом закона Фурье ГУ III рода можно записать следующим образом

,

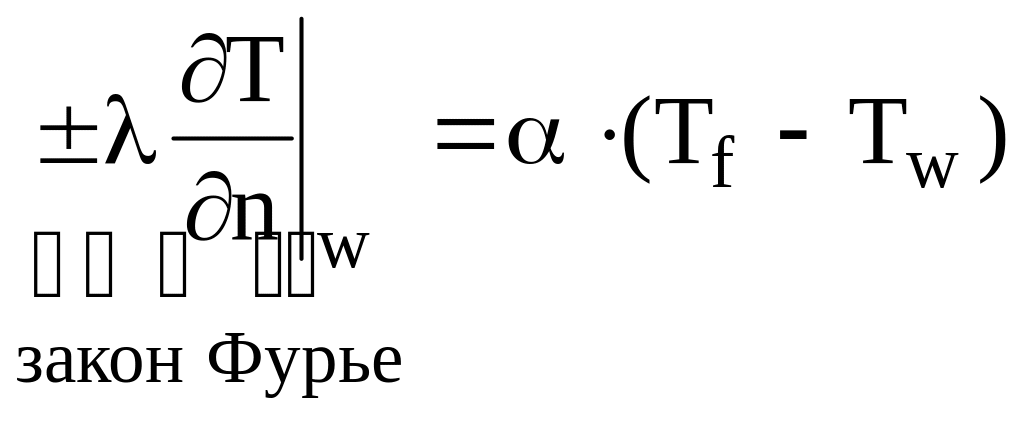где знак + или – в законе Фурье зависит от выбора начала системы координат.

В расчетах теплопроводности используют безразмерную форму записи граничных условий третьего рода : , где – безразмерная температура; – безразмерная координата, перпендикулярная поверхности теплообмена; R – характерный или определяющий размер тела; – критерий Биó (Biot); λ_w – коэффициент теплопроводности твердого тела.

Граничные условия IV рода задают условия теплообмена на границе идеального контакта двух тел, состоящих из разного вещества с разными физическими свойствами

10.Теплопроводность при стационарном режиме.Передача теплоты через плоскую стенку.Многослойная стенка.

-Наиболее распространенный случай –теплопроводность через однослойную плоскую стенку,длина и ширина которой бесконечно велики по сравнения с толщиной .Стенка имеет во всех своих частях одинаковую толщину, причем температуры поверхностей t’cт и t’’ст поддерживаются постоянными т.е. являются изотермами поверхностям. Температура меняется только в направлении, перпендикулярном к плоскости стенки,которое принимаем за ось х. Коэффициент теплопроводности постоянен для всей стенки.При стационарном тепловом режиме температура в любой точке тела неизменна и ене зависит от времени. Тогда получаем диф.уравнение теплопроводности после сокращения коэффициента температуропроводности: .

После интегрирования получаем t=Ax+B.При постоянном коэффициенте теплопроводности это уравнение прямой линии.Следовательно,закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.Количество теплоты передаваемой теплопроводностью через плоскую стенку,прямо пропорционально коэффициенту теплопроводности стенки ей площади, промежутку времени, разности температур на наружных поверхностях стенки и обратно пропорционально толщине стенки. Тепловой потом зависит не от абсолютного значения температур,а от их разности ,называемой температурным напором.В действительности коэффициент теплопроводности реальеных тел зависит от температуры и закон изменения температур выражается кривой линией.Если коэффициент теплопроводности зависит от температуры в незначительной степени,то на практике закон изменения температур считают линейным. Получаем: разделив и интегрируя получаем при этом плотность теплового потока может определяться из уравнения : .Уравнения температурной кривой в стенке получается путем решения квадратного уравнения относительно t и подстановки значения C из уравнения :

Из этого следует,что температура внутри стенки изменяется по кривой.Если коэффициент b отрицателен,то кривая будет направлена выпуклостью вниз,если b положителен,то выпуклостью вверх.

-Расчетную формулу теплопроводности сложной стенки при стационарном состоянии можно вывести из уравнения теплопроводности для отдельных слоев считая что тепловой поток,проходящий через любую изотермную поверхность неоднородной стенки один и тот же. Определяем тепловой поток для каждого слоя: .Решая эти уравнения относительно разности температур и складывая, получаем или для любого числа слоев: .Отношение называют термическим сопротивлением слоя,а величину -полным термическим сопротивлением многослойной плоской стенки.Эквиваолентный коэффициент теплопроводности многослойной стенки равен коэффициенту теплопроводности однородной стенки той же толщины,с теми же температурами поверхности и пропускающей тот же тепловой поток. Величина зависит от термических сопротивлений и толщин отдельных слоев.Температура в каждом слое стенки при постоянном коэффициенте теплопроводности изменяется по линейному закону,а для многослойной плоской стенки температурный график представляет собой ломаную линию.