33. Закон распределения функции случайной величины

Одной из важных задач в теории вер-стей является определение з-на распределения ф-и одной или нескольких случайных величин. Для непрерывн случ вел Х: пусть случ вел-на У есть ф-я от Х, т.е. Y=f(X) – строго монотонна, непрерывна и диф-ма на отрезке [a,b], f(a)=c, f(b)=d. Полагаем что f ’(x)>0.

Тогда ф-я р-я G(y) сл вел У: , где g(y) – плотность вер-сти сл вел У.

Для нахождения числовых хар-стик сл вел Y = f(X) не обязательно знать з-н ее р-я, достаточно знать з-н р-я аргумента: М(У)=M[f(X)]=∫f(x)φ(x)dx, D(Y)=D[f(X)]=∫ [f(x)-M(Y)]^2 φ(x)dx (интегралы считать от - ∞ до +∞). Из множ-ва задач на составление з-на р-я ф-и неск случ вел важное для практики значение имеет задача опред-я з-на р-я суммы двух случ вел Z= X+ Y. В случае, если Х и Y - независимые случ вел-ны, говорят о композиции з-нов р-я.

43.Числовые характеристики выборочной характеристики и их свойства.

Для того чтобы вычислить числовые характеристики признака, представленного интервальным вариационным рядом, следует перейти к дискретному вариационному ряду, заменив интервалы их серединными значениями.

54. Метод наименьших квадратов.

Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, называется методом наименьших квадратов.

31. Линейная зависимость двух случайных величин

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, такие как корреляционный момент и коэффициент корреляции. Характеристикой зависимости между случайными величинами и служит математическое ожидание произведения отклонений и от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:

Д ля вычисления корреляционного момента дискретных величин используют формулу

а для непрерывных величин – формулу:

Корреляционный момент двух независимых случайных величин и равен нулю.

Коэффициент корреляции: Математическое ожидание каждой из случайных величин

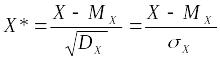и равно нулю, а дисперсия – единице. Ковариация и называется коэффициентом корреляции случайных величин и (обозначается ).

32. Условные числовые характеристики двумерной случайной величины. Регрессия.

Числовые хар-ки: M(X)=∫∫x φ(x,y)dxdy (M(Y) аналогично), D(X)=∫∫(x-M(X))^2 dxdy (для D(Y) аналогично, все интегралы считать от - ∞ до +∞). Условное мат. ожидание случайной величины Y при X = х, т.е. Mх(Y), есть ф-я от х, называемая ф-цией регрессии или просто регрессией Y по Х; аналогично Му(Х) - регрессия X по Y. Графики этих функций наз-тся линиями регрессии YпoХ и ХпоУ. (Регрессия- зависимость среднего значения какой-либо случайной величины от некоторой другой величины или от нескольких величин)

34. З-н больших чисел

З-н больших чисел – раздел теор вер-сти, в кот изуч-ся факторы, влияющие на измерение чисел стремящихся к бесконечности. Это ряд строгих матем.теорем, каждая из которых при тех или иных условиях устанавливают факт приближения средних характеристик СВ к некоторым неопределенным постоянным.ЗБЧ(предельные теоремы): 1. Поведение средних характеристик СВ при многократном появлении опыта. 2. Теоремы, которые определяют характер СВ. 1. сходимость по вероятности: Последовательность СВ {х_n(w)} сходится по вероятности СВ х(w) и обозначается lim х_n(w)= х(w) х_n(w)→ х(w). Если для любого Е> 0, lim P((х_n(w))<E)=1 2. сходимость по распределению: {х_n(w)}, х_n(w)→х сходится, если lim F_n(x)=f(x), где F_n – функция распределения СВ, х(w) – функция распределения СВ(Х).