28) Продольная несимметрия

Цель расчета – определение токов и напряжений в ветвях повреждений в заданных точках. Этот расчет необходим для выбора элементов СЭС, РЗА.

К продольной несимметрии относятся:

1. разрыв одной фазы трехфазной цепи;

2. разрыв двух фаз трехфазной цепи.

Продольную несимметрию представляют как включение в каждую фазу электрической системы неодинаковых сопротивлений. Разрыв в фазе тождественен включению в месте разрыва, источника напряжения, равного падению напряжения на концах разорванной фазы.

Здесь также эффективно применение МСС , в соответствии с которым расчетные соотношения можно выразить через симметричные составляющие тока и напряжения фазы А, принятой за основную.

где E_A - суммарная ЭДС источников питания, действующая только в схеме прямой последовательности;

Z_1рез , Z_2рез , Z_0рез – результирующие сопротивления отдельных последовательностей, относительно места нарушения несимметрии.

§1. Разрыв одной фазы трехфазной цепи

Р азрыв одной фазы трехфазной цепи показан на рис.28.

Граничные условия:

(32)

Рис.28. Трехфазная сеть с разрывом фазы А в месте L - L

Д ля анализа аварийного режима в разрыв вводят источник продольного напряжения (рис.29)

Рис.29. Исходная схема для анализа нарушения продольной симметрии при разрыве фаза А в месте L – L’

Составляют схемы замещения отдельных последовательностей.(Рис.30)

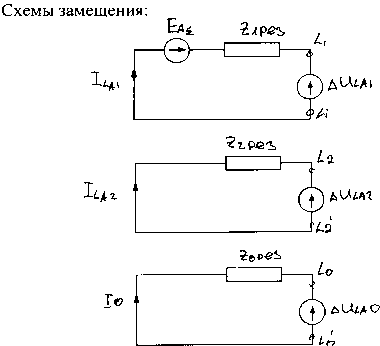
Рис.30. Схемы прямой, обратной и нулевой последовательности при обрыве фазы А вместе L – L’

Из сравнения падений напряжений для неповрежденных фаз выраженных через симметричные составляющие, следует

Таким образом, на основе симметричных составляющих граничные условия (32) могут быть записаны в виде:

По этим уравнениям может быть синтезирована комплексная схема замещения рассматриваемого нарушения продольной симметрии (рис. 31).

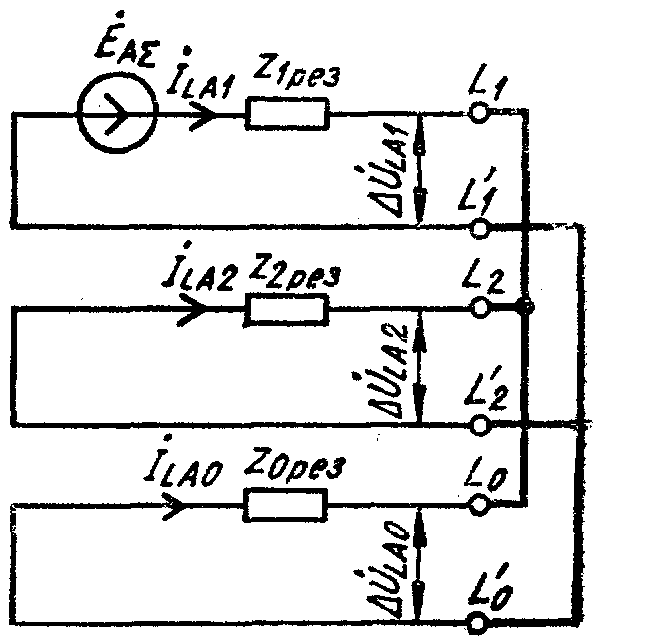
Р ис.31. Комплексная схема замещения нарушения продольной симметрии при разрыве фазы А

По ней составляют расчетные выражения для определения тока прямой последовательности

и падения напряжения прямой последовательности в месте разрыва

вносимое в схему замещения прямой последовательности относительно зажимов L — L' ветвями схем замещения обратной и нулевой последовательностей (см. рис.31).

С учетом (33), а также второго и третьего уравнений (31) токи обратной и нулевой последовательностей, протекающие в других ветвях комплексной схемы замещения (см. рис.31), определяются выражениями

Токи обратной и нулевой последовательностей могут быть выражены через показатели комплексной схемы замещения следующим образом:

В соответствии с (33) и (31) напряжение источника продольного напряжения, включаемого в месте повреждения, определяется выражением

Полученные расчетные соотношения (33) — (41) представляли собой уравнения связи симметричных составляющих параметров режима особой фазы.

Токи и напряжения других фаз выражаются через оператор фазы с использованием уравнений (29) и (30).

Напряжения в любой точке сети определяются по расчетным выражениям токов (35), (39) и (40) с использованием преобразований комплексной схемы замещения (см. рис.31) относительно рассматриваемой точки сети для вычисления сопротивлений связи данной точки с источником питания.